Yixuan Yang , Doo-Soon Park , Fei Hao , Sony Peng , Hyejung Lee and Min-Pyo Hong
Detection of Maximal Balance Clique Using Three-way Concept Lattice
Abstract: In the era marked by information inundation, social network analysis is the most important part of big data analysis, with clique detection being a key technology in social network mining. Also, detecting maximal balance clique in signed networks with positive and negative relationships is essential. In this paper, we present two algorithms. The first one is an algorithm, MCDA1, that detects the maximal balance clique using the improved three-way concept lattice algorithm and object-induced three-way concept lattice (OE-concept). The second one is an improved formal concept analysis algorithm, MCDA2, that improves the efficiency of memory. Additionally, we tested the execution time of our proposed method with four real-world datasets.
Keywords: Formal Concept Analysis , Maximal Balanced Clique , Signed Networks , Three-Way Concept
1. Introduction
In response to the demands of the Fourth Industrial Revolution era, many researchers are directing their attention to social network structures analysis in computer science, with the cliques emerging as a very popular research direction in social network structure mining. Vilakone et al. [1,2] used clique detection and standardized cumulative gains to solve some problems in the movie recommendation system. However, detecting the maximal clique and balanced cliques in social networks, are not only applicable to social media software, but also can be applied to other domains, such as the Internet of Things (IoT), healthcare, biology, and more.
Meanwhile, maximal clique detection can be used to detect the structure of proteins, which can prevent or control diseases. For this reason, we can find a group of the most suitable medical specialists for a target patient to provide the best medical treatment through remote consultation.
In many existing works, cliques are typically detected in undirected and unweight graphs [3,4]. However, some social networks contain positive and negative relationships between users, and are called signed social networks. Significantly, there are some studies about mining cliques from the social network [5,6], while several studies have been conducted using signed social networks [7-9]. However, few studies have used formal concept analysis (FCA) to do the maximal balanced clique detection in the signed social networks.
To solve the maximal balanced clique detection problem (MBCP), it is necessary to propose some more efficient methods; therefore, this paper focuses on designing the modified three-way concept algorithms, which are more suitable for the signed social networks.
The organization of our paper is described as follows. We introduce the research background and our motivation in Section 1, with the related works and some terminologies introduced in Section 2, and then the maximal balanced clique detection algorithms for signed social networks are presented in Section 3. To show its validness and efficiency, we have applied it to some real datasets and synthetic datasets in Section 4; meanwhile, we also compare the experimental results with other methods. Finally, the conclusion and future works are provided in Section 5.
2. Basic Notions
In this section, we introduce several basic concepts of the signed networks, maximal balanced cliques, and three-way concept lattice.
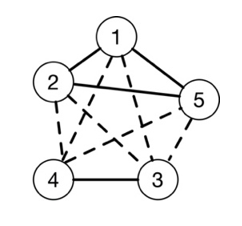
A signed social network G is characterized as a graph structure, and the graph composed of nodes and edges. The nodes represent the users in social network, and edges have weights, which are positive and negative values and represent positive and negative relationships, respectively. For example, as shown in Fig. 1, this is a signed social network, and there are five nodes in a signed social network G, between these nodes, the solid lines represent the positive edges, and the dotted lines represent the negative edges.
To explain the definitions of the maximal balanced network [7], FCA [10], and three-way concept [11,12], we present here an example that lets us easily understand the original FCA and three-way concept.
Definition 1 ([TeX:] $$\text { Operator } ^\leq \text { and } ^\geq$$ [11]). Let F = (O, A, I) be a formal context. For any [TeX:] $${\mathrm{X}, \mathrm{M}} \subseteq \mathrm{O}, \mathrm{Y}, \mathrm{N} \subseteq \mathrm{A},$$ a pair of three-way operators are defined mathematically below:
(3)
[TeX:] $$(\mathrm{Y}, \mathrm{N})^{\geq}=\left\{\mathrm{x} \in \mathrm{O} \mid \mathrm{x} \in \mathrm{Y}^{\downarrow} \text { and } \mathrm{x} \in \mathrm{N}^{\downarrow *}\right\}=\mathrm{Y}^{\downarrow} \cap \mathrm{N}^{\downarrow *}$$
(4)
[TeX:] $$(\mathrm{X}, \mathrm{M})^{\geq}=\left\{\mathrm{a} \in \mathrm{A} \mid \mathrm{a} \in \mathrm{X}^{\uparrow} \text { and } \mathrm{a} \in \mathrm{M}^{\uparrow *}\right\}=\mathrm{X}^{\uparrow} \cap \mathrm{M}^{\uparrow *}$$Based on Definition 1, three-way concepts are defined in detail as follows.
Definition 2 (Three-way concepts [11]). The three-way concepts including two parts: AE-concept and OE-concept.
AE-concept: Let F = (O, A, I) be a formal context. For any [TeX:] $$\mathrm{X}, \mathrm{M} \subseteq \mathrm{O}, \mathrm{Y} \subseteq \mathrm{A},((\mathrm{X}, {\mathrm{M}}), \mathrm{Y})$$ is called an attribute-induced three-way concept (AE-concept), if and only if [TeX:] $$(\mathrm{X}, \mathrm{M})^{\geq}=\mathrm{Y} \text { and } \mathrm{Y}^{\leq}=(\mathrm{X}, \mathrm{M}) \text {, }$$ where (X, M ) is called the extent and Y is called the intent of ((X, M ), Y). The set of all AE-concepts of F = (O, A, I) can form a lattice by some partial order structure.
OE-concept: Let F = (O, A, I) be a formal context. For any [TeX:] $$\mathrm{X} \subseteq \mathrm{O}, {\mathrm{Y}, \mathrm{N}} \subseteq \mathrm{A},(\mathrm{X},(\mathrm{Y}, \mathrm{N}))$$ is called an object-induced three-way concept (OE-concept), if and only if [TeX:] $$\mathrm{X}^{\leq}=(\mathrm{Y}, \mathrm{N}) \text { and }(\mathrm{Y}, \mathrm{N})^{\geq}=\mathrm{X}$$, where X is called the extent and (Y, N) is called the intent of (X, (Y, N)). The set of all OE-concepts of F = (O, A, I) can form a lattice by some partial order structure, and this lattice is called OE lattice.
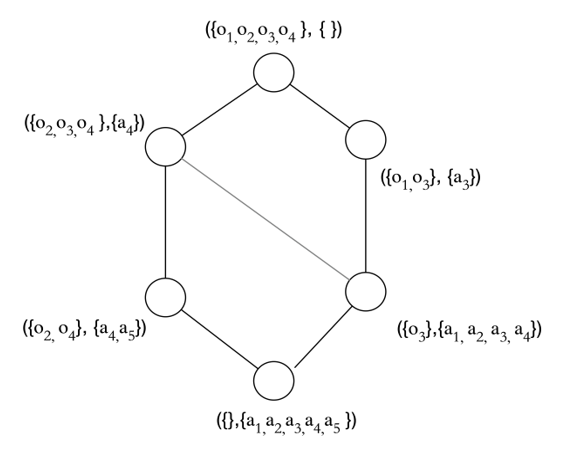
Example 1. Table 1 is a formal context F. Table 2 is a supplemental formal context [TeX:] $$\mathrm{F}^{\mathrm{c}}$$ for Table 1. Among them, O represents the object of the form context, and A represents the attribute corresponding to object O. Through the traditional FCA method mentioned above, using the formal context of Tables 1 and 2 and the operations in Definition 1 above, we can obtain all object sets with the same attributes (i.e., concepts, which are represented by nodes in Fig. 2), and form a concept lattice of the formal context [TeX:] $$\mathrm{F}^{\mathrm{c}}$$, which is represented as Fig. 2.
Table 1.
| [TeX:] $$\mathbf{O} \times \mathbf{A}$$ | [TeX:] $$\mathbf{a}_1$$ | [TeX:] $$\mathbf{a}_2$$ | [TeX:] $$\mathbf{a}_3$$ | [TeX:] $$\mathbf{a}_4$$ | [TeX:] $$\mathbf{a}_5$$ |
|---|---|---|---|---|---|
| [TeX:] $$\mathbf{o}_1$$ | 1 | 1 | 0 | 1 | 1 |
| [TeX:] $$\mathbf{o}_2$$ | 1 | 1 | 1 | 0 | 0 |
| [TeX:] $$\mathbf{o}_3$$ | 0 | 0 | 0 | 0 | 1 |
| [TeX:] $$\mathbf{o}_4$$ | 1 | 1 | 1 | 0 | 0 |
Table 2.
| [TeX:] $$\mathbf{O} \times \mathbf{A}$$ | [TeX:] $$\mathbf{a}_1$$ | [TeX:] $$\mathbf{a}_2$$ | [TeX:] $$\mathbf{a}_3$$ | [TeX:] $$\mathbf{a}_4$$ | [TeX:] $$\mathbf{a}_5$$ |
|---|---|---|---|---|---|
| [TeX:] $$\mathbf{o}_1$$ | 0 | 0 | 1 | 0 | 0 |
| [TeX:] $$\mathbf{o}_2$$ | 0 | 0 | 0 | 1 | 1 |
| [TeX:] $$\mathbf{o}_3$$ | 1 | 1 | 1 | 1 | 0 |
| [TeX:] $$\mathbf{o}_4$$ | 0 | 0 | 0 | 1 | 1 |
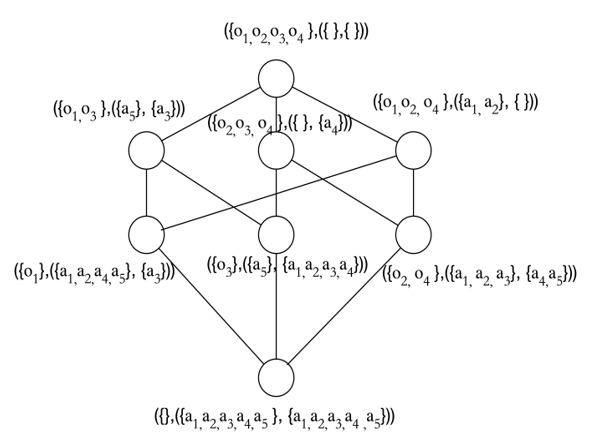
Similar to the acquisition process in Fig. 2, the concept lattice of the formal context F can be obtained. Based on the formal contexts F and [TeX:] $$\mathrm{F}^{\mathrm{c}}$$, the OE-concept lattice is obtained by Definition 2, which is shown in Fig. 3.
3. Proposed Maximal Cliques Detection Approach
This section proposes two novel methods for maximal balanced clique detection in the signed networks. The first method obtains the modified OE lattice through the existing three-concept lattice algorithm using the improved three-way formal context and modified formal context. We have detected all maximal balanced cliques in the OE lattice. The second method is to optimize the first method to improve the detection of the maximal balanced cliques using the traditional FCA along with the modified formal context.
In the signed social networks, we applied the formal context and supplemental formal context for representing the positive and negative relationships between nodes, which is denoted as modified formal context.
Definition 3 (Modified formal context). If a signed network g has nodes {v1,v2,...,vn}, each node vi represents an object and its attribute, and edge e = (vi, vj) is the relationship between the objects and attributes, [TeX:] $$\text { I or } \mathrm{I}^{\mathrm{c}}$$. If [TeX:] $$\text { e } \in \mathrm{E}+$$, notes I(vi, vj) = 1, if [TeX:] $$\text { e } \in \mathrm{E}-$$, notes [TeX:] $$\text {I}^\mathrm{c}(\mathrm{vi}, \mathrm{vj})=1.$$ Then, if F = (O, A, I) and [TeX:] $$\mathrm{F}^{\mathrm{c}}=\left(\mathrm{O}, \mathrm{A}, \mathrm{I}^{\mathrm{c}}\right)$$ are modified formal contexts, they can be represented as two adjacency matrixes containing only 0 and 1.
(5)
[TeX:] $$\mathrm{M}(\mathrm{F})=\left\{\begin{array}{l} m_{i j}=1, \text { if }\left(v_i, v_j\right) \in E^{+} \text {and } i \neq j \\ m_{i j}=1, \text { if } i=j \\ m_{i j}=0, \text { if }\left(v_i, v_j\right) \notin E^{+} \text {and } i \neq j \end{array}\right.$$
(6)
[TeX:] $$\mathrm{M}\left(\mathrm{F}^{\mathrm{c}}\right)=\left\{\begin{array}{l} m_{i j}=1, \text { if }\left(v_i, v_j\right) \in E^{-} \text {and } i \neq j \\ m_{i j}=1, \text { if } i=j \\ m_{i j}=0, \text { if }\left(v_i, v_j\right) \notin E^{-} \text {and } i \neq j \end{array}\right.$$Definition 4 (Modified OE and AE). Taking the modified formal context and supplemental formal context for generating OE-concept and AE-concept in a three-way concept algorithm, we can get a modified OE lattice (denoted MOE) and a modified AE lattice (denoted MAE).
Maximal cliques detection approach 1 (MCDA1): The modified formal context F = (O, A, I) and supplemental formal context [TeX:] $$\mathrm{F}^{\mathrm{c}}=\left(\mathrm{O}, \mathrm{A}, \mathrm{I}^{\mathrm{c}}\right)$$ are used to obtain modified three-way concept lattices, MOE and MAE. When there is a concept in MOE and X = Y, i.e., (X, (X, N)), X and N form the maximal balanced clique represented by {X, N}, and (X, (X, N)) is the maximal balanced OE-concept.
Theorem 1. Let MOE be the OE-concept lattice of modified formal contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^c \text {. }$$ For any [TeX:] $$(\mathrm{X}, (\mathrm{Y}, \mathrm{N})) \in \mathrm{MOE}$$, if X = Y, it is denoted as (X, (X, N)), {X, N} is the maximal balanced clique, such that [TeX:] $$\forall \mathrm{u},\mathrm{v} \in \mathrm{X} \text { or } \mathrm{u}, \mathrm{v} \in \mathrm{N} \rightarrow(\mathrm{u}, \mathrm{v}) \in \mathrm{E}^{+}$$, and [TeX:] $$\forall \mathrm{u} \in X, \mathrm{v} \in \mathrm{N} \text { or } \mathrm{u} \in \mathrm{N}, \mathrm{v} \in X \rightarrow(\mathrm{u}, \mathrm{v}) \in \mathrm{E}^{-}$$.
Proof. There is [TeX:] $$(\mathrm{X}, \mathrm{Y}) \in \mathrm{FC}(\mathrm{F}) \text { and }(\mathrm{M}, \mathrm{N}) \in \mathrm{FC}\left(\mathrm{F}^c\right) \text {, and }(\mathrm{X},(\mathrm{Y}, \mathrm{N})) \in \mathrm{MOE} \text {. }$$
1) If X = Y, we can get [TeX:] $$\mathrm{(X, X)}=\mathrm{(X, Y)} \in \mathrm{F C(F)}$$, while (X, X) is an equi-concept in FC(F) and (X, X) is a maximal clique and [TeX:] $$\forall \mathrm{u}, \mathrm{v} \in \mathrm{X},(\mathrm{u}, \mathrm{v}) \in \mathrm{E}^{+}$$.
2) Because of [TeX:] $$(\mathrm{X},(\mathrm{Y}, \mathrm{N})) \in \mathrm{MOE}$$, if X = Y, we can get [TeX:] $$(\mathrm{X},(\mathrm{Y}, \mathrm{N}))=(\mathrm{X},(\mathrm{X}, \mathrm{N})) \in \mathrm{MOE}$$. According to Definition 4, for a modified OE-concept [TeX:] $$(\mathrm{X},(\mathrm{X}, \mathrm{N})),\left(\mathrm{X}, {\mathrm{N})^{\geq}}=\mathrm{X}^{\downarrow} \cap \mathrm{N}^{\downarrow *}=\mathrm{X}\right. \text {. }$$ Based on the definitions of concept, [TeX:] $$\mathrm{X}^{\downarrow}=\mathrm{Y}=\mathrm{X}, \mathrm{N}^{\downarrow^*}=\mathrm{M},$$, then [TeX:] $$\mathrm{X}^{\downarrow} \cap \mathrm{N}^{\downarrow *}=\mathrm{X} \cap \mathrm{M}=\mathrm{X}$$. Then, [TeX:] $$\mathrm{X} \subseteq \mathrm{M}.$$ Because of [TeX:] $$(\mathrm{M}, \mathrm{N}) \in \mathrm{FC}\left(\mathrm{F}^{\mathrm{c}}\right)$$, [TeX:] $$\forall \mathrm{u} \in \mathrm{M}, \mathrm{v} \in \mathrm{N} \text { or } \mathrm{u} \in \mathrm{N}$$, [TeX:] $$\mathrm{v} \in \mathrm{M} \rightarrow(\mathrm{u}, \mathrm{v}) \in \mathrm{E}^{-}$$, we can get that [TeX:] $$\forall \mathrm{u} \in \mathrm{X} \subseteq \mathrm{M}, \mathrm{v} \in \mathrm{N} \text { or } \mathrm{u} \in \mathrm{N}, \mathrm{v} \in \mathrm{X} \subseteq \mathrm{M} \rightarrow(\mathrm{u}, \mathrm{v}) \in \mathrm{E}^{-}$$.
The working process of MCDA1 is described in Algorithm 1. In Algorithm 1, the sets of maximal balanced cliques and modified OE-concept are initialized in Line 1. Line 3 constructs formal contexts F and Fc for the signed social network G. The Construct _MFC is given by Algorithm 2. Line 4 follows the rules of the traditional three-way concept algorithm according to the modified contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$ to get the modified OE lattice. Lines 5-8 use Theorem 1 to detect the maximal balanced cliques from MOE. Finally, set the MBC returns from Line 9.
Algorithm 1

In Line 1 of Algorithm 2, we initialized the matrices of both contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$ to 0. Lines 3-10 construct two matrices, the three-way formal context F, and the supplemental formal context [TeX:] $$\mathrm{F}^{\mathrm{c}}$$, according to Definition 12. Line 11 returns the three-way contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$.
Here, we present an example that lets us easily understand how to use an MCDA1 for the maximal balanced clique detection in the signed social networks.
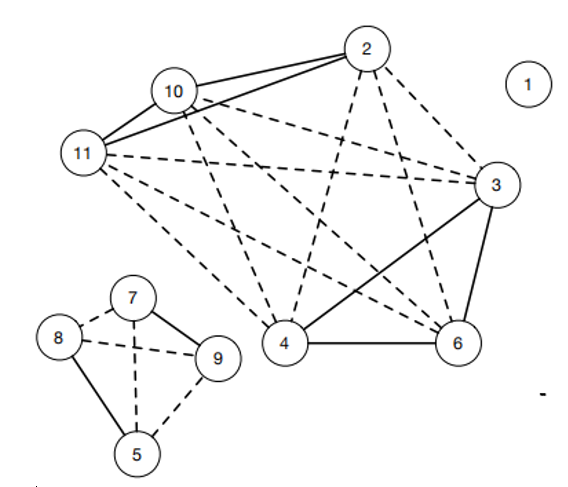
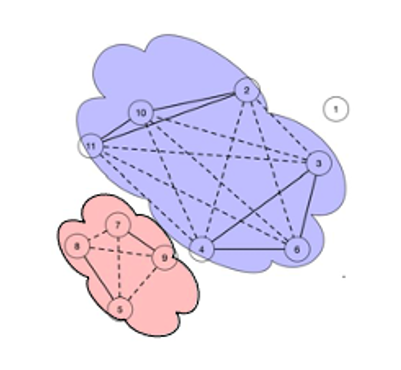
Example 2. Fig. 4 shows a signed social network graph, which includes 11 nodes, eight positive edges, and 13 negative edges. The modified OE lattice of the signed social network G is obtained using Algorithms 1 and 2, meanwhile, Fig. 5 lists all OE-concepts of the modified OE lattice. The extents and intents of each concept are separated by "#"". According to Theorem 1, it is easy to find four suitable OE-concepts in the following list: (3, 4, 6) # ((3, 4, 6), (2, 10, 11)); (5, 8) # ((5, 8), (7, 9)); (2, 10, 11) # ((2, 10, 11), (3, 4, 6)); (7, 9) # ((7, 9), (5, 8)). Moreover, we obtained two maximal balanced cliques: {{3, 4, 6}, {2, 10, 11}}; {{5, 8}, {7, 9}}.
In Fig. 6, the purple and orange parts are two maximal balanced cliques with vertex label numbers consistent with the above results.
Due to the three-way concept method being a NP-completed problem, so the MCDA1 also suffered from a high time complexity problem because if there are massive nodes in a signed social network, this method cannot quickly obtain the modified OE lattice, making it unable to quickly obtain the maximal balanced cliques. Therefore, we analyzed the characteristics of OE-concepts based on the three-way concept method, and proposed another detection algorithm of maximal balanced cliques that can be quickly obtained, starting directly from the traditional concept analysis with the formal context and supplemental formal context, which is described as MCDA2.
Maximal cliques detection approach 2 (MCDA2). The modified formal context F = (O, A, I) and supplement context [TeX:] $$\mathrm{F}^{\mathrm{c}}=\left(\mathrm{O}, \mathrm{A}, \mathrm{I}^{\mathrm{c}}\right)$$ are used as two input formal contexts for the traditional FCA method. According to the input contexts and formal context analysis, we obtained two modified formal concept lattices, [TeX:] $$\Omega(\mathrm{F}) \text { and } \Omega\left(\mathrm{F}^{\mathrm{c}}\right)$$.
Principle 1. Compare with each concept in [TeX:] $$\Omega(\mathrm{F}) \text { and } \Omega\left(\mathrm{F}^{\mathrm{c}}\right)$$. When there are two concepts (X, Y) and (C, D) in the [TeX:] $$\Omega(\mathrm{F}) \text { and } \mathrm{X=Y} \text { and }\mathrm{ C=D} \text {, }$$ they are equi-concepts. Concurrently, if there is (X, D) in the [TeX:] $$\Omega\left(\mathrm{F}^{\mathrm{c}}\right)$$, X is the extent of (X, Y) and (X, D), D is the intent of (C, D) and (X, D), then X and D form a maximal balanced clique, which is denoted as {X, D}.
Algorithm 3

Algorithm 3 explains the above processes. In Algorithm 3, Line 1 initializes the sets of maximal balanced cliques, equi-concept, concept lattice [TeX:] $$\Omega(\mathrm{F}), \Omega\left(\mathrm{F}^\mathrm{c}\right)$$. Line 3 constructs the formal contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$ for the signed social network G, while the construct-MFC is given in Algorithm 2. Lines 4-5 obtain the concept lattice of formal contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$. Lines 6-8 obtain the set of equi-concept. Lines 9-12 detect maximal balanced cliques through Approach 2 based on Principle 1. Finally, the set of maximal balanced clique will return in Line 9.
Example 3. Fig. 7 shows the concept lattice of contexts [TeX:] $$\mathrm{F} \text { and } \mathrm{F}^{\mathrm{c}}$$. If we follow Approach 2, we can get four equi-concepts (the number of extent or intent is more than one): (3, 4, 6)#(3, 4, 6); (2, 10, 11)#(2, 10, 11), (5, 8)#(5, 8), (7, 9)#(7, 9). We used the previous four equi-concepts to obtain the four concepts in lattice [TeX:] $$\Omega\left(\mathrm{F}^\mathrm{c}\right)$$, and followed the rules in Approach 2: ((3, 4, 6) # (2, 10, 11)); ((5, 8) # (7, 9)); ((2, 10, 11) # (3, 4, 6)); ((7, 9) # (5, 8)). Then, we obtained two maximal balanced cliques: {{3, 4, 6}, {2, 10, 11}}; {{5, 8}, {7, 9}}. As shown in Fig. 6, the purple and orange parts are two maximal balanced cliques with vertex labels numbers consistent with the above results.
4. Experiment and Performance Analysis
This section presents experimental datasets and execution times. The experimental environment consists of the macOS Catalina operating system and two Intel 2.3 GHz Quad-Core Intel Core i5, RAM 16G, and uses the programming language Python 3.8. In this section, we used two approaches proposed in Section 3 to perform experiments.
The modified three-way concept lattice method can deal with symmetric and asymmetric formal contexts, but the modified FCA can only handle the symmetric formal context of maximal balanced detection. Therefore, we first tested approach 1 (modified three-way concept) using three different real-life asymmetric datasets. We used large symmetric real-life datasets to compare approach 1 to approach 2 (modified FCA).
4.1 Time Efficiency Analysis
4.1.1 Asymmetric dataset
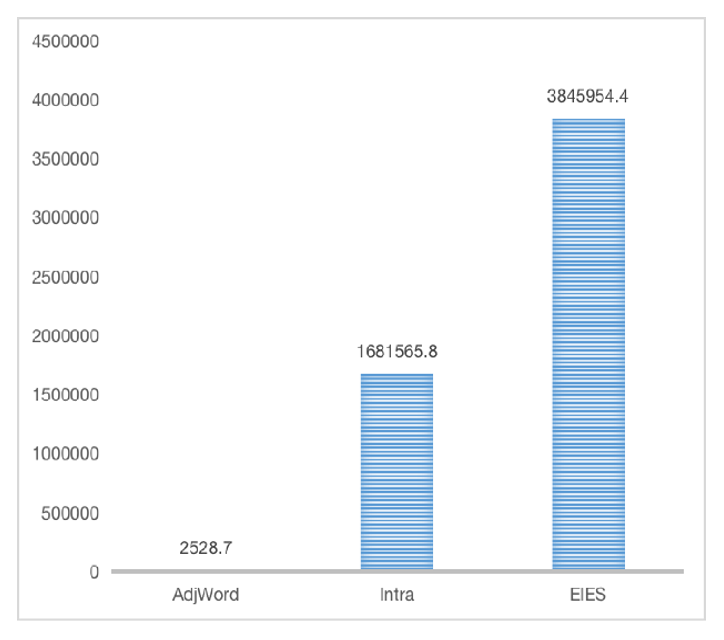
In this part, we tested the run-time of three asymmetric datasets by MCDA1. There are three real-life datasets (Table 3), and the first dataset is 11 nodes from AdjWordNet [13], which involves synonyms and antonyms of certain words. The second dataset is a network of intra-organization [14], which is a dataset of a consulting company (46 employees) and records the requests a frequent quantity of information or advice among employees. The third dataset is Freeman’s EIES networks [15], which includes some personal relationships among 46 researchers.
Table 3.
| Number of nodes | Number of edges | |
|---|---|---|
| AdjWordNet | 11 | 15 |
| Intra | 46 | 879 |
| EIES | 46 | 695 |
As shown in Fig. 8, comparing the run-time among different datasets, the first dataset is less than that of the other two datasets. Thus, although we can see that MCDA1 is highly sensitive to the number of nodes and edges, it has the advantage of being able to compute the asymmetric formal context that is not limited to social network datasets.
4.1.2 Symmetric dataset
In this part, we tested the run-times of MCDA1 and MCDA2 by using the Slashdot dataset [16]. Slashdot is known as a specific user community, whose website has the ability to allow users to submit the latest news on the site and for editors to evaluate the content. Additionally, the Slashdot dataset entails friends and relationships between Slashdot users. Slashdot includes 77,350 nodes and 516,575 edges, but in this paper, we take only the first 2,000 nodes of the dataset and experiment in groups of different sizes.
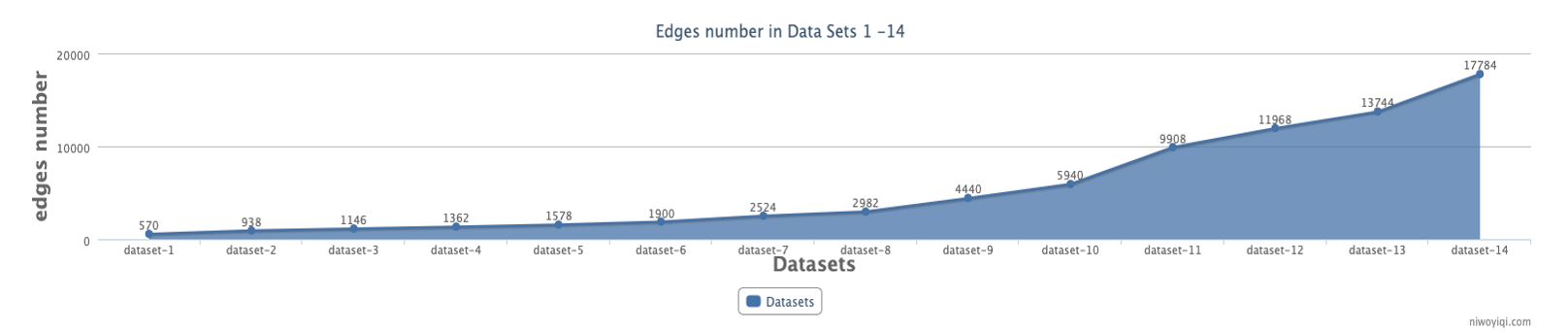
We transform the relationships of a dataset into undirected relationships without considering the positive or negative relationship in a single direction to obtain a symmetric matrix that simulates an undirected weighted social network (Table 4). The edges number of each dataset is counted in Fig. 9.
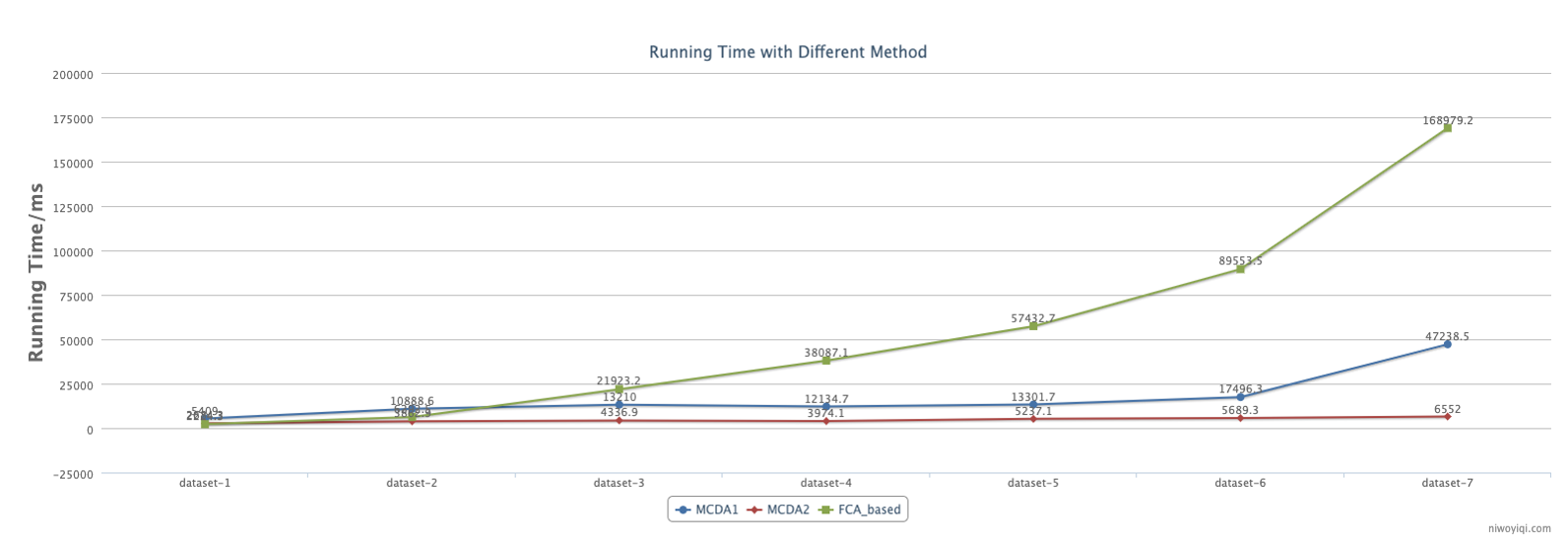
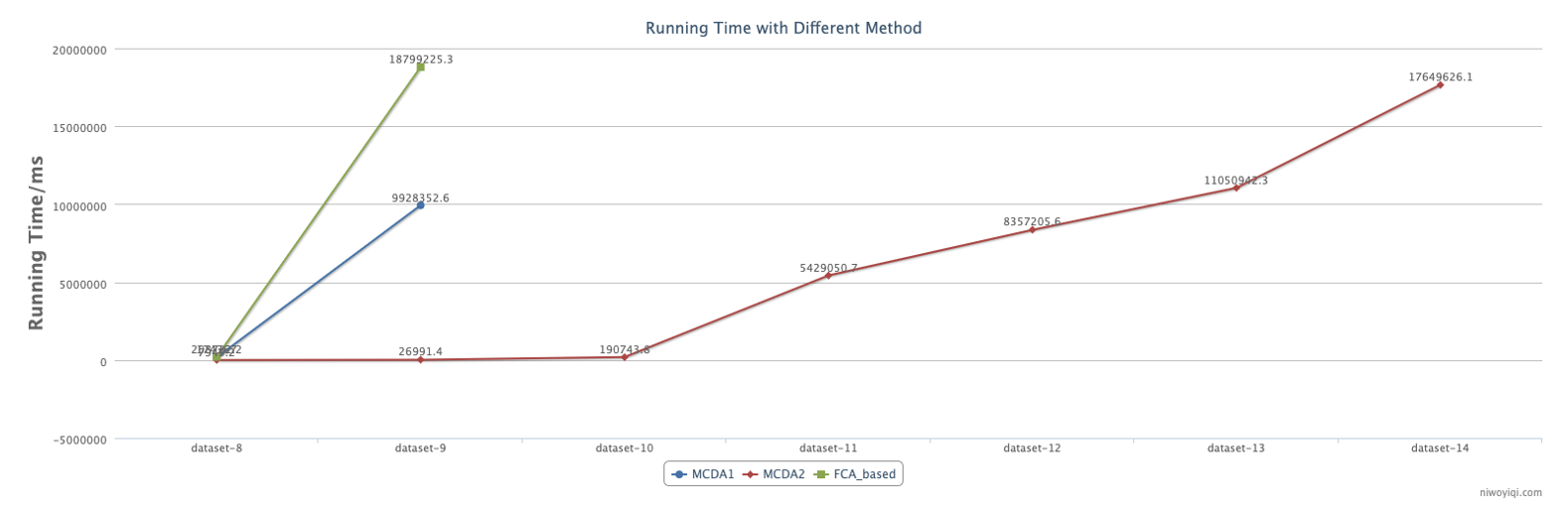
Fig. 10 shows the comparison of the run-time on datasets 1-7 with the MCDA1, MCDA2 and FCA-based methods (which was proposed in [17]). Note that the algorithm only works for detecting a k-balance clique in the signed social network to make this algorithm comparable with our algorithms, and we made a small improvement on the algorithm. The blue line shows the run-time by the MCDA1, the red line shows the run-time by the MCDA2, and the green line shows the run-time by the FCA-based method. According to Fig. 11, it is observed that the execution time of the MCDA2 method significantly outperforms the other two methods.
Table 4.
| Dataset | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| Number of nodes | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1300 | 1500 | 1700 | 2000 |
4.2 Case Study of Detecting Synonyms in Vocabulary
In Section 4.1, we used three datasets to compare the time efficiency of the approaches and demonstrate the utility of our methods. However, we not only focused on the time efficiency of our method, but also cared about the utility. Hence, in the case study, we applied the AdjWordNet dataset to our method, and the results illustrate the utility of our method. AdjWordNet is downloaded from WordNet (www://wor dnet.priceton.edu). This dataset contains 117,000 synonyms and antonyms of certain words. Among them, the synonyms are linked by positive edges, while the antonyms are linked by negative edges, without the presences of edges between unrelated words.
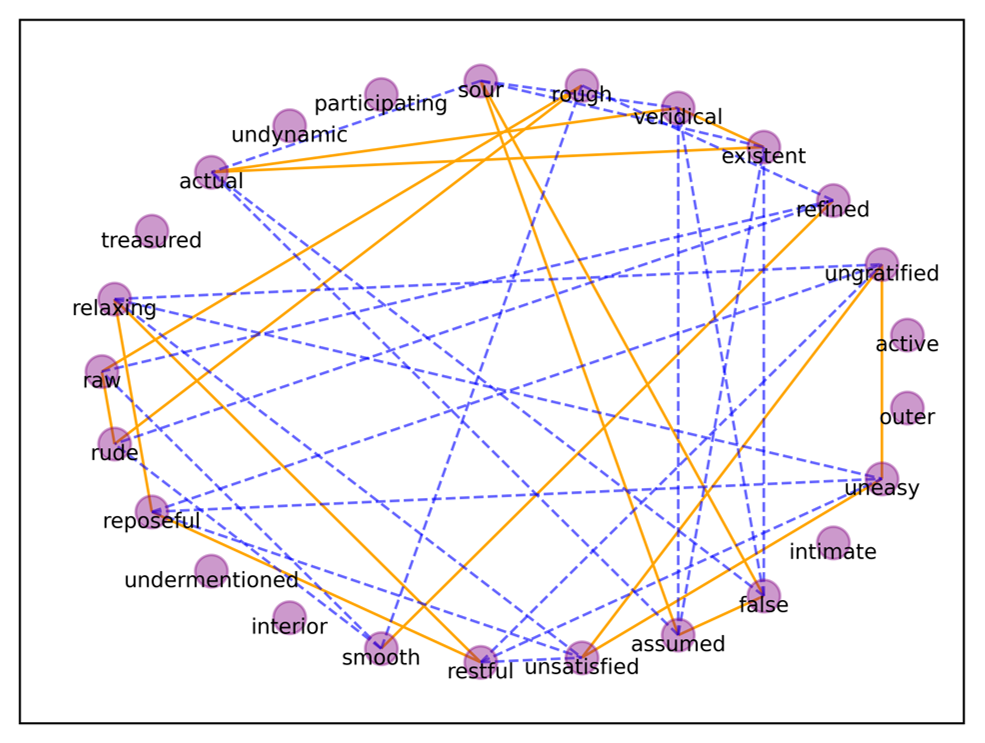
In our case study, to observe the flow and effect of our method more clearly, we selected 25 words randomly from AdjWordNet. The graph of the 25 words is shown in Fig. 12 and Table 5.
Table 5.
| raw | rough | rude | relaxing | refined |
| interior | smooth | assumed | false | intimate |
| uneasy | ungratified | restful | reposeful | unsatisfied |
| outer | existent | veridical | actual | sour |
| participating | undynamic | active | undermentioned | treasured |
Fig. 12 shows the 25 words and their relationships, and among them, the orange solid line shows that the two words are synonyms, while the blue dotted line represents that the two words are antonyms, with the words without a line bearing no relationship. Table 5 contains the vocabulary list of the nodes in Fig. 12.
The results which are obtained by our method is shown in Table 6. In this table, the words in [TeX:] $$\mathrm{C}_1 \text { and } \mathrm{C}_2$$ are denoted as synonyms for each line, respectively and each column [TeX:] $$\mathrm{C}_1 \text { and } \mathrm{C}_2$$ represents a group of two antonyms.
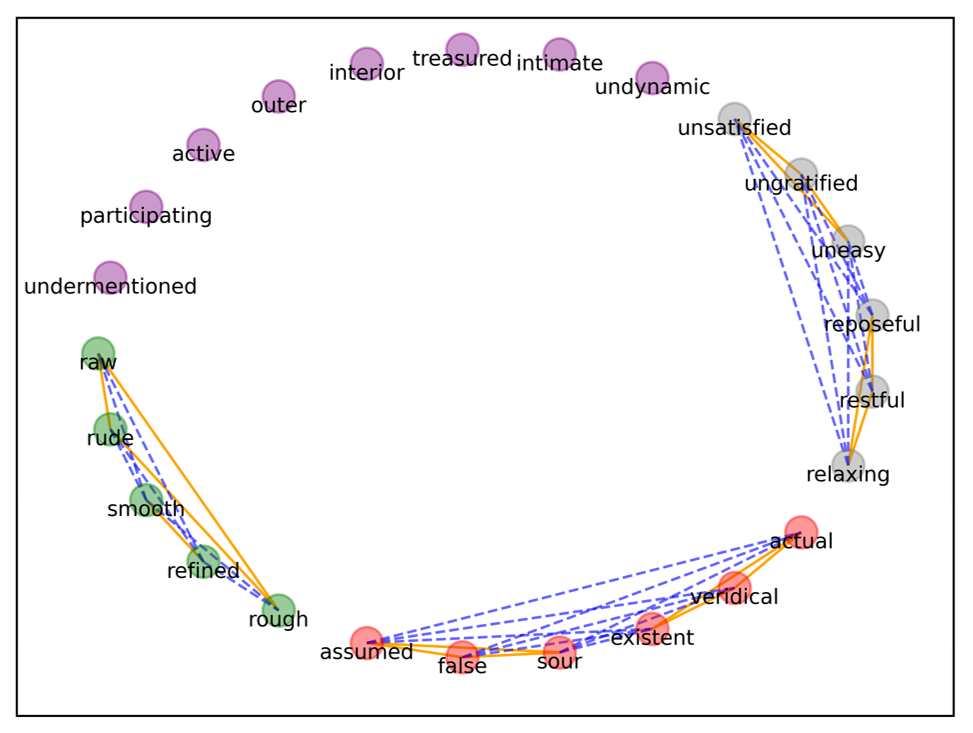
We visualized the three maximal balanced cliques in Table 6, as shown in Fig. 13, which denotes the following: the green nodes are the first maximal balanced cliques, the orange nodes are the second maximal balanced cliques, the gray nodes are the third maximal balanced cliques, and the remaining purple nodes are the vocabulary with no synonyms and antonyms in this dataset.
5. Conclusion
In this paper, we proposed an improved three-way concept algorithm MCDA1 and an improved formal concept algorithm MCDA2 for detecting the maximal balanced clique in signed social networks. To demonstrate the feasibility of the proposed method, in the performance evaluation, four real-life signed social networks were used to detect maximal balanced cliques, and synonyms and antonyms were used on the AdjWorldNet dataset. Also, we found that the two methods provide both advantages and dis-advantages. Accordingly, MCDA1 method has a wider application range on asymmetric datasets, whereas the MCDA2 method has a faster computation speed and higher efficiency. This proposed method can be applied in detecting synonyms and antonyms in a vocabulary list, detecting social network user groups, and analyzing the protein molecular structure. Moreover, it can be applied to more scenarios in the future. Going forward, we plan to solve the problem of long run-times in the MCDA1.
Biography
Yixuan Yang
https://orcid.org/0000-0002-9334-566XShe received her B.Sc. degree in Software Engineering from Taiyuan University of Technology, China (2017), and her M.Sc. degree in Software Engineering from Shaanxi Normal University, China (2020). She is currently pursuing her Ph.D. degree at Soonchunhyang University, South Korea. Her research interests include social computing, community detection and formal concept analysis.
Biography
Doo-Soon Park
https://orcid.org/0000-0002-2776-8832He received his Ph.D. in Computer Science from Korea University in 1988. Currently, he is a professor in the Department of Computer Software Engineering at Soonchun-hyang University, South Korea. He is Dean of Graduate School at Soonchunhyang University, Director of BK21 FOUR Well-Life Big Data at Soonchunhyang Univer-sity. He was President of KIPS from 2015 to 2015. He was editor in chief of JIPS from 2009 to 2012. He has served as an organizing committee member of international conferences including, BIC 2021, MUE 2021, WorldIT 2021, CSA 2020, BIC 2019, FutureTech 2019, WorldIT 2019, FutureTech 2018, BIC 2018. His research interests include social computing, big data analysis. He is a member of ACM, KIPS, and KMS.
Biography
Fei Hao
https://orcid.org/0000-0001-5288-5523He received the B.Sc. degree in Information and Computing Science and the M.Sc. degree in Computer Software and Theory from Xihua University, China, in 2005 and 2008, respectively, and the Ph.D. degree in Computer Science and Engineering from Soonchunhyang University, South Korea, in 2016. Since 2016, he has been with Shaanxi Normal University, Xi’an, China, where he is an Associate Professor. He is currently taking a Marie Sklodowska-Curie Individual Fellowship at the University of Exeter, Exeter, United Kingdom. His research interests include social computing, ubiquitous computing, big data analysis and processing and mobile cloud computing.
Biography
Hyejung Lee
https://orcid.org/0000-0001-8359-1608She received her B.S., M.S., and Ph.D. in computer science engineering from Soonchunhyang University, South Korea, in 1997, 2000, and 2006, respectively. She is currently an assistant professor with the Department of Innovation and Convergence, Hoseo University (HSU), Asan, South Korea. Currently, her research interests contain data mining, parallel processing, big data processing, and computer education.
Biography
References
- 1 P . Vilakone, X. Xinchang, and D. S. Park, "Movie recommendation system based on users' personal information and movies rated using the method of k-clique and normalized discounted cumulative gain," Journal of Information Processing Systems, vol. 16, no. 2, pp. 494-507, 2020.doi:[[[10.3745/JIPS.04.0169]]]
- 2 P . Vilakone, K. Xinchang, and D. S. Park, "Personalized movie recommendation system combining data mining with the k-clique method," Journal of Information Processing Systems, vol. 15, no. 5, pp. 1141-1155, 2019.doi:[[[10.3745/JIPS.04.0138]]]
- 3 L. Y uan, L. Qin, X. Lin, L. Chang, and W. Zhang, "Diversified top-k clique search," The VLDB Journal, vol. 25, pp. 171-196, 2016.doi:[[[10.1007/s00778-015-0408-z]]]
- 4 F. Hao, G. Min, Z. Pei, D. S. Park, and L. T. Yang, "K-clique community detection in social networks based on formal concept analysis," IEEE Systems Journal, vol. 11, no. 1, pp. 250-259, 2017.doi:[[[10.1109/JSYST.2015.2433294]]]
- 5 S. Kumar, F. Spezzano, V . S. Subrahmanian, and C. Faloutsos, "Edge weight prediction in weighted signed networks," in Proceedings of 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 2016, pp. 221-230.doi:[[[10.1109/icdm.2016.0033]]]
- 6 J. Kunegis, A. Lommatzsch, and C. Bauckhage, "The Slashdot Zoo: mining a social network with negative edges," in Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 2009, pp. 741-750.doi:[[[10.1145/1526709.1526809]]]
- 7 Z. Chen, L. Y uan, X. Lin, L. Qin, and J. Yang, "Efficient maximal balanced clique enumeration in signed networks," in Proceedings of the Web Conference 2020, Taipei, Taiwan, 2020, pp. 339-349.doi:[[[10.1145/3366423.3380119]]]
- 8 J. Salminen, M. Hopf, S. A. Chowdhury, S. G. Jung, H. Almerekhi, and B. J. Jansen, "Developing an online hate classifier for multiple social media platforms," Human-centric Computing and Information Sciences, vol. 10, article no. 1, 2020. https://doi.org/10.1186/s13673-019-0205-6doi:[[[10.1186/s13673-019-0205-6]]]
- 9 S. Ahmad, M. Z. Asghar, F. M. Alotaibi, and I. Awan, "Detection and classification of social media-based extremist affiliations using sentiment analysis techniques," Human-centric Computing and Information Sciences, vol. 9, article no. 24, 2019. https://doi.org/10.1186/s13673-019-0185-6doi:[[[10.1186/s13673-019-0185-6]]]
- 10 Y . Yang, F. Hao, B. Pang, K. Qin, Z. Pei, and B. Li, "A quick algorithm on generating concept lattice for attribute-incremental streaming data," in Proceedings of 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; and IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 2019, pp. 2811-2816.doi:[[[10.1109/hpcc/smartcity/dss.2019.00394]]]
- 11 S. Yang, Y . Lu, X. Jia, and W. Li, "Constructing three-way concept lattice based on the composite of classical lattices," International Journal of Approximate Reasoning, vol. 121, pp. 174-186, 2020.doi:[[[10.1016/j.ijar.2020.03.007]]]
- 12 F. Hao, Y . Yang, G. Min, and V . Loia, "Incremental construction of three-way concept lattice for knowledge discovery in social networks," Information Sciences, vol. 578, pp. 257-280, 2021.doi:[[[10.1016/j.ins.2021.07.031]]]
- 13 G. A. Miller, WordNet: An Electronic Lexical Database. Cambridge, MA: MIT Press, 1998.doi:[[[10.2307/417141]]]
- 14 R. L. Cross and A. Parker, The Hidden Power of Social Networks: Understanding How Work Really Gets Done in Organizations. Boston, MA: Harvard Business School Publishing, 2004.doi:[[[10.1111/j.1467-9620.2005.00619.x]]]
- 15 S. C. Freeman and L. C. Freeman, "The networkers network: a study of the impact of a new communications medium on sociometric structure," School of Social Sciences, University of California, CA, 1979.custom:[[[https://books.google.co.kr/books/about/The_Networkers_Network.html?id=sN9NGwAACAAJ&redir_esc=y]]]
- 16 J. Leskovec, D. Huttenlocher, and J. Kleinberg, "Signed networks in social media," in Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Atlanta, GA, 2010, pp. 1361-1370.doi:[[[10.1145/1753326.1753532]]]
- 17 F. Hao, S. S. Yau, G. Min, and L. T. Yang, "Detecting k-balanced trusted cliques in signed social networks," IEEE Internet Computing, vol. 18, no. 2, pp. 24-31, 2014.doi:[[[10.1109/mic.2014.25]]]