Qian Wang , Shi Dong and Hamad Naeem
Data Mining for Uncertain Data Based on Difference Degree of Concept Lattice
Abstract: Along with the rapid development of the database technology, as well as the widespread application of the database management systems are more and more large. Now the data mining technology has already been applied in scientific research, financial investment, market marketing, insurance and medical health and so on, and obtains widespread application. We discuss data mining technology and analyze the questions of it. Therefore, the research in a new data mining method has important significance. Some literatures did not consider the differences between attributes, leading to redundancy when constructing concept lattices. The paper proposes a new method of uncertain data mining based on the concept lattice of connotation difference degree (c_diff). The method defines the two rules. The construction of a concept lattice can be accelerated by excluding attributes with poor discriminative power from the process. There is also a new technique of calculating c_diff, which does not scan the full database on each layer, therefore reducing the number of database scans. The experimental outcomes present that the proposed method can save considerable time and improve the accuracy of the data mining compared with U-Apriori algorithm.
Keywords: Concept Lattice , Difference Degree , Frequent Items , Uncertain Database
1. Introduction
One of the most significant aspects of data mining is the extraction of frequent item sets, and it is also the basic content of the research of data mining. In conventional database, the data is determined, and the probability of emergence is 100%. In the traditional database, the data is determined, and the probability of emergence is 100%, e.g., application fields such as sensor information transfer and moving object data management. Uncertain data is now widely available in the real world. The research of uncertain data cannot be ignored [1]. A hot research subject in data mining is how to mine frequent patterns in uncertain data.
In order to mine the frequent item sets of data, some algorithms have been proposed and widely used. Among them, the Apriori algorithm and the FP-growth algorithm [2-5] are the two most classical algorithms for mining frequent itemsets. These two algorithms cannot deal with the frequent item set mining of uncertain data, because the existence and the precision of the data are not accurate. In order to mine the frequent item sets of uncertain data, some algorithms have been proposed [6]. The most important algorithms are the U-Apriori algorithm, which is based on the Apriori algorithm, and the UFgrowth algorithm, which is based on the FP-growth algorithm. U-Apriori algorithm is proposed by Chui et al. U-Apriori algorithm is the expected support as support, instead of the large set of data to determine the degree of support [7]. However, when mining frequent itemsets, the U-Apriori algorithm still has issues; it requires more than one scan of the database, which affects the efficiency of the algorithm. UFgrowth algorithm is the same as the same probability of the project to be combined, as a tree node, which leads to a large number of redundant nodes [8]. The U-Apriori algorithm has some shortcomings; therefore, research has proposed a concept lattice based on the concept lattice of uncertain data mining, referred to as the UD-Apriori algorithm, which greatly improves efficiency.
In the determination of data, data mining association rules based on concept lattice, a lot of scholars have conducted in-depth research, and it is a hot issue that has been studied [9]. But in the mining of uncertain data, few scholars have combined the concept lattice and the association rules together. Potentially high average-utility sequential pattern mining (PHAUSPs) is a new approach to sequential pattern mining that overcomes the limitations of the previous prospective high-utility sequential pattern mining framework by considering the sequence size [10], which can provide a fair measure of the patterns than the previous works [11] proposing a list-based pattern mining method over uncertain data considering an importance condition in this paper. Raman et al. [12] proposes a new framework which to deal with sequences in uncertain databases considering both weight and support constraints. Lee and Yun [13] provides a precise and efficient method for mining uncertain frequent patterns based on unique data structures and mining approaches, which can also guarantee the correctness of the mining results without any false positives. Lee et al. [14] describes and analyses current state-of-the-art approaches based on tree structures and offers a novel uncertain frequent pattern mining strategy.
Although some scholars have introduced the concept lattice theory, the importance of the concept of the concept lattice is equal and the importance of the same, without taking into account the differences in the content of the case, resulting in low efficiency and long-time [15]. Aiming at the importance of concept lattice connotation differences, put forward the concept of a new concept, connotation difference, to construct the concept lattice will be greatly reduced in the lattice of uncertain frequent item sets in data, because the attribute difference is low structure does not need to be involved in the case, to a certain extent reduces the combination explosion phenomenon. On the other hand, constructing the concept lattice is a condition to scan the database without need of each layer, so that it can save the time of constructing concept lattice. First, provide some definitions, and then describe the construction process of concept lattices, highlighting the differences among them. Furthermore, present the uncertain data mining algorithm, explaining the differences in connotation based on concept lattices. The experiments confirm that the algorithm is effective.
The contributions of this paper are as follows:
· Proposed a new method of uncertain data mining based on the concept lattice of connotation difference degree (c_diff) that reduces the number of database scans.
Experimental outcomes with varying system parameters demonstrate substantial performance improvement of our method over other competing methods. For example, the UD-Apriori algorithm minimizes the running time consumption compared with the U-Apriori algorithm in the case of different threshold values.
The rest of this paper is organized as follows. Section 2 discusses uncertain data. Section 3 proposes a new method of construction method of concept lattice based on difference degree. Mining of uncertain data based on difference concept lattice is described in Section 4. The experimental results are presented in Section 5. Several experiments have been conducted to improve the accuracy of predictions. Finally, the paper concludes in Section 6.
2. Uncertain Data
In the research of uncertain data, the most common model is the possible world mode. The model evolves many possible world instances from an uncertain database (called to determine database instance), and the sum of probabilities of these instances is 1 [1]. For example, a patient is caused by lack of exercise and irregular diet. But the probability of these two causes of different patients is different. The probability of A patients caused by lack of exercise is 90%, and irregular diet is 10%. The probability of B patients caused by lack of exercise is 70%, and irregular diet for 30%.
In a deterministic database, if itemset X represents frequent itemsets, Support(X) indicates the support of item set X, then Support(X) must be larger than the minimum threshold given by the user. In the uncertain database, every possible world exists in the form of probability, and it is not possible to accurately calculate the number of the item sets, as shown in Table 1. Table 2 is the background of uncertain data mining in Table 1. Therefore, in the uncertain database, expected support exp(X) instead of Support(X) [16].
Table 1.
| Tid | Items |
|---|---|
| T1 | (A,0.7), (B,0.7), (D,0.5) |
| T2 | (B,0.6), (C,0.8) |
| T3 | (A,0.6), (B,0.8), (C,0.6), (D,0.6) |
| T4 | (A,0.8), (B,0.9), (D,0.8) |
| T5 | (A,0.9), (B,0.2), (C,0.9) |
| T6 | (C,0.9) |
Table 2.
| Tid | A | B | C | D |
|---|---|---|---|---|
| T1 | 0.7 | 0.7 | 0 | 0.5 |
| T2 | 0 | 0.6 | 0.8 | 0 |
| T3 | 0.6 | 0.8 | 0.6 | 0.6 |
| T4 | 0.8 | 0.9 | 0 | 0.8 |
| T5 | 0.9 | 0.2 | 0.9 | 0 |
| T6 | 0 | 0 | 0.9 | 0 |
Definition 1 (Support probability): In the uncertain data, if [TeX:] $$P\left(x, T_i\right)$$ is the probability of possible world [TeX:] $$T_i$$, and the expectation support of itemset is x exp(X), [17] is deduced and proved:
Definition 2 (Probability frequent itemset): In the uncertain data, if the itemset X is a frequent itemset, then exp(X) must be greater than the minimum threshold (min_thre), which is given by the user. Otherwise, itemsets X is not frequent itemsets.
Definition 3. The formal context of data mining is three tuple K = (G, M, I), where G stands for a collection of objects, M is a set of attributes, and I is a two element relationship between G and M. If an object g ∈ G, attribute m ∈ M, the two relationship between them can be expressed by gIm.
A formal context K = (G, M, I), Object set [TeX:] $$A \subseteq G$$, and Attributes [TeX:] $$B \subseteq M$$ defined the mapping:
Definition 4. Two tuple C(A,B) represents the concept of formal context K=(G, M, I), which is to meet f(A) = B and g(B) = A. So, A is the extension of the concept, B is the connotation of the concept.
Property 1. If the formal context K = (G, M, I) exists A, A1, [TeX:] $$A2 \subseteq G$$ and B, B1, [TeX:] $$B2 \subseteq M$$
(1) [TeX:] $$A 1 \subseteq A 2 \Rightarrow f(A 1) \supseteq f(A 2), B 1 \subseteq B 2 \Rightarrow g(B 1) \supseteq g(B 2).$$
(2) [TeX:] $$A \subseteq g(f(A)), B \subseteq f(g(B)).$$
Definition 5. Super concept and sub concept. The given formal context K=(G, M, I), formal concept C1(A1, B1) and C2(A2, B2), if [TeX:] $$A 1 \subseteq A 2 \text { or } B 2 \subseteq B 1,$$ then concept C1 is a sub concept of concept C2, Concept C2(A2, B2) is the parent concept of concept C1(A1, B1), namely (A1, B1) ≤ (A2, B2). In the formal context, the formation of partial relation their parent concept—the concept lattice is called concept lattice [18], namely L(K). If concept C3(A3,B3) does not relationship (A1, B1) ≤ (A3, B3) ≤ (A2, B2), then the concept C1 is the direct sub concept of concept C2, and concept C2(A2, B2) is the direct parent concept of concept C1(A1, B1).
Definition 6. Connotation difference degree. In the uncertain database, the probability of any attribute are not the same that is to say their importance is different, especially in the data mining association rules. The criticality of these properties is different, so the difference between the attribute difference is called connotation difference degree(or connotation attribute difference), namely c_diff.
Property 2. If an attribute appears too many times, its difference will be small.
For example: if A, B, C, D, E, and F are attributes in the uncertain database that A, C ⇒ E and A, D, C ⇒ E existed, which determines the appearance of attribute E and C. If there is A, B ⇒ F and B, D ⇒ F, the attribute F will appear as long as the attribute B appears. The attribute F does not play a decisive role, it will not be of much significance as the antecedent of the rule.
Property 3. If the expectation support of some attribute is small, it will also have a small connotation difference degree.
3. Construction Method of Concept Lattice based on Difference Degree
There is a great relationship between attribute difference and expectation support. In the uncertain database, the expectation support is low and the attribute difference will be low. The low degree of attribute difference will lead to over-fitting in the process of constructing concept lattice, thus, the attributes of low difference degree will be removed, and not involved in the construction of concept lattice. It is not only to reduce the time complexity of concept lattice construction, but also to reduce the complexity of the association rules of uncertain data.
In the process of constructing concept lattice, based on the above definition of these two rules:
1) In the first layer of the concept lattice, the sum of the corresponding attribute probabilities is initialized to their property difference degree c_diff. If the c_diff minimum support threshold [TeX:] $$\varphi$$ is deleted, the attribute is removed from the concept lattice.
(2) The second and the following layers of the concept lattice are calculated by Formula 1, and the expectation support exp(X) is obtained. If exp(X) minimum support threshold [TeX:] $$\varphi$$, then c_diff = exp(X). Otherwise, it is eliminated from concept lattice.
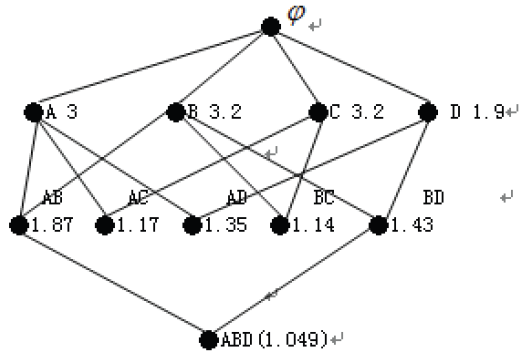
For example, Table 1 is an uncertain database, and Table 2 is the corresponding mining background. If the threshold [TeX:] $$\varphi=0.5$$, the difference degree concept lattice based on Table 2, as shown in Fig. 1.
Fig. 1 shows the specific process of constructing concept lattice. Second layer of Fig. 1 is the mode AB.
Therefore, the pattern is not scanned and skipped.
Mode CD:
Therefore, the pattern CD is removed from the concept lattice.
4. Mining of Uncertain Data based on Difference Concept Lattice
Association rules are rules such as X ⇒ Y, where [TeX:] $$\mathrm{X}=\mathrm{m}_{\mathrm{i} 1} \cup \mathrm{m}_{\mathrm{i} 2} \cup \ldots \cup \mathrm{m}_{\mathrm{ij}}$$ [TeX:] $$\mathrm{Y}=\mathrm{m}_{\mathrm{i} 1} \cup \mathrm{m}_{\mathrm{i} 2} \cup \ldots \cup \mathrm{m}_{\mathrm{j},}, \mathrm{m}_{\mathrm{ij}}\cup \mathrm{M}$$ is attribute, and [TeX:] $$\mathrm{X} \cap \mathrm{Y}=\emptyset \text {. }$$
The concept of concept lattice L(K) is C1(A1, B1) ≤ C2(A2, B2), and the expectation support of concept C1 and concept C2 is [TeX:] $$\alpha \text { and } \beta(\alpha \geq \varphi) \text {. }$$ Concept C2 is the parent concept of the concept C1, which can be concluded [TeX:] $$\beta \geq \varphi \text {. }$$ If the attribute set is represented by B1-B2 in B1 and not in B2, then there is the B2 ⇒ B1-B2 rule. Its support is α. For a given threshold [TeX:] $$\varphi$$, it is easy to obtain some meaningful association rules by concept lattice.
Given the definition of the concept lattice, it is easy to realize the mining of uncertain data. Based on the above definition of these two rules:
1) If there is a (A1, B1) ≤ (A2, B2) relationship between the concept C1(A1, B1) and C2(A2, B2) of concept lattice L(K), it can be concluded that the association rules of B2 ⇒ B1-B2. Otherwise, it does not exist (A1, B1) ≤ (A2, B2), and it has the non-empty common sub concept C(A, B), then it can get the association rules of B1 ⇒ B-B1 and the association rules of B2 ⇒ B-B2.
2) If there is not a (A1, B1) ≤ (A2, B2) relationship between the concept C1(A1, B1) and C2(A2, B2) of concept lattice L(K), it has the common sub concept C(A, B) but there are no non empty, and it can be concluded that the association rules of B1 ⇒ B2-B and B2 ⇒ B1-B; otherwise, it can be concluded that the association rules of B2-B ⇒ B1 and B1-B ⇒ B2.
The mining of uncertain data rules based on concept lattice can extract concept lattices from different levels, and the purpose is to obtain the association rules of any length to meet the needs of users at different levels. There are still some problems in the generation process of concept lattice based on attribute difference. For example, the low degree of expectation support is not involved in the construction of the lattice, and the deletion. In the process of lattice construction, the expectation of attribute is too high to be involved. In order to ensure the integrity of association rules mining, the attribute expectation is too high to be deleted. It should be part of the frequent item sets, and participate in the rule construction. The algorithm flow chart shown in Fig. 2. The detail proposed algorithm presents with pseudo-codes in Algorithm 1.
5. Experimental Results
To ensure the correctness of the experiment, the data set and the U-Apriori algorithm used to run the program were downloaded from the URL http://dbgroup.cs.tsinghua.edu.cn/liyan/u_mining.tar.gz. The experiment utilized a deterministic data set, which was converted into an uncertain data set with evenly distributed uncertainty. The experimental platform consisted of a computer with a Pentium 2.10 GHz CPU, 1GB of memory, and Windows 7 OS, using C++ language to implement the UD-Apriori and UApriori algorithms for solving the frequent itemsets mining problem. The experiment compared the running times under different minimum support thresholds.
Experiment 1: The minimum support threshold is 0.1, 0.2, 0.3, 0.5, 0.8, 0.9, the total number of things used to test the uncertainty of the data, the running time of the situation of the 300000. According to the user to select a different threshold (Support Threshold), running time changes, as shown in Fig. 3.
Fig. 3 shows the UD-Apriori algorithm and U-Apriori algorithm running time comparison. The experimental results display that the UD-Apriori algorithm is more effectual than the U-Apriori algorithm.
Experiment 2: The minimum support threshold values were 0.2, 0.3, 0.4, 0.5, 0.6, and 0.9. Using a dataset with a total of 100K items, the experiment tested how the running time for mining uncertain data itemsets changes with these threshold values. With the selection of different threshold (Support Threshold), the running time changes, as shown in Fig. 4. Fig. 4 is the running time of the UD-Apriori algorithm and U-Apriori algorithm. Fig. 3 experimental outcomes display that the UD-Apriori algorithm minimizes the running time consumption compared with the U-Apriori algorithm in the case of different threshold values.
The results of Experiment 1 and Experiment 2 show that the amount of data is proportional to the time of the algorithm. The greater the amount of data, the faster the running time. These two experiments show that the UD-Apriori algorithm is of high operating efficiency. In particular, the larger the amount of data, the UD-Apriori algorithm is better than the U-Apriori algorithm.
Experiment 3: In order to further verify the effectiveness of the UD-Apriori algorithm, the proposed algorithm is superior to U-Apriori algorithm. From the comparison of the accuracy of the data mining, data mining using the UD-Apriori technique is more accurate than U-Apriori algorithm, as shown in Fig. 5.
6. Conclusion
At present, the concept lattice has been used by many researchers to study the rules of association, and they have achieved significant progress. However, there is less research on association rules analysis in uncertain data mining. The previous researchers are not sure directly correspond to frequent itemsets in data and the connotation of concept lattice, and scan the database one time at a time, wasting time. In this paper, the method of constructing the concept lattice based on the connotation difference and the difference degree can effectively solve the existing problems.
Biography
Biography
Shi Dong
https://orcid.org/0000-0003-4616-6519He received Ph.D. in Computer Science from Southeast University in 2013. He is a visiting scholar in Washington University in St. Louis and a distinguished professor with Zhoukou Normal University. He has published more than 100 papers in top conferences and journals. He is a reviewer of IEEE Journal on Selected Areas in Communications, IEEE Transactions on Parallel and Distributed Systems, IEEE/ACM Transactions on Networking; IEEE Transactions on Neural Networks and learning systems; Computer Networks; IEEE Transactions on Network Science and Engin-eering; IEEE Transactions on Industrial Informatics; IEEE Internet of Things Journal. He also is an associate editor for IEEE Systems Journal, Physical Communication, IET Networks, IET Wireless Sensor Systems, IEICE Transactions on Communications, Journal of Artificial Intelligence and Soft Computing Research, and International Journal on Artificial Intelligence Tools. As a guest editor, he has organized special issues of several journals including (JEI, CMC and Applied Sciences). He is currently the leader of Network and Information Security Innovative Science and Technology Team of Henan Province, the leader of the Provincial Key Discipline of Computer Application Technology of Henan Province, a CCF distinguished member, and a supervisor of the master's degree students of the Wuhan Textile University. His major interests are network management, network security.
Biography
Hamad Naeem
https://orcid.org/0000-0003-1511-218XHe received the Bachelor’s degree in Computer Systems Engineering from the Bahauddin Zakariya University (NFC IET) Multan, Pakistan, in 2012, Master’s degree in Software Engineering from Chongqing University Chongqing, China, in 2016, and the Doctoral degree in Software Engineering from Sichuan University Chengdu, China, in 2019. During his employment at Neijiang Normal University Neijiang Sichuan China, he received the Top 10 RESEARCHER AWARD for the period of 2019 to 2020. He is currently serving as an Associate Professor with the School of Computer Science and Technology, Zhoukou Normal University Zhoukou, China. He is working as an Associate Editor of BMC Research Note Springer and reviewer board member of IJDCF, IGI Global. He has been a reviewer for leading journals and also a TPC member of several conferences. He has published more than 30 SCI and EI articles in various renowned journals of the Elsevier, Springer, Wiley, and IEEE publishers. He is on collaborative research with Al-Balqa Applied University Jordan on various issues in cyber security and medical image processing domains. His research directions include computer virus detection, software security, cyber-security, medical image processing and machine intelligence.
References
- 1 M. Gao, "Data provenance management and similarity query over uncertain data," M.S. thesis, Fudan University, Shanghai, China, 2011.custom:[[[-]]]
- 2 S. Rao and P . Gupta, "Implementing improved algorithm over APRIORI data mining association rule algorithm," International Journal of Computer Science and Technology (IJCST), vol. 3, no. 1, pp. 489-493, 2012.custom:[[[-]]]
- 3 J. Han and M. Kamber, Data Mining: Concepts and Techniques. San Francisco, CA: Morgan Kaufmann, 2001.custom:[[[-]]]
- 4 H. Zhao, C. Cai, and X Li, "Overview of association rules Apriori mining algorithm," Journal of Sichuan University of Science and Technology (Natural Science Edition), vol. 24, no. 1, pp. 66-70, 2011. https://doi.org/10.3969/j.issn.1673-1549.2011.01.019doi:[[[10.3969/j.issn.1673-1549.2011.01.019]]]
- 5 L. Chi, "A two-class classification mining algorithm based on the FP-growth algorithm and its application," M.S. thesis, Qingdao University, Qingdao, China, 2012.custom:[[[-]]]
- 6 Z. Liu and R. Chang, "Fast algorithm of frequent itemset mining based on matrix from uncertain data," Journal of Nanjing University of Science and Technology (Natural Science Edition), vol. 39, no. 4, pp. 420425, 2015. https://doi.org/10.14177/j.cnki.32-1397n.2015.39.04.007doi:[[[10.14177/j.cnki.32-1397n.2015.39.04.007]]]
- 7 J. Wang, L. Zhang, Q. Deng, F. Wang, and Y . Wang, "Survey on algorithm of mining frequent itemsets from uncertain data," Computer Engineering and Applications, vol. 47, no. 20, pp. 121-125, 2011. https://doi.org/10.3778/j.issn.1002-8331.2011.20.035doi:[[[10.3778/j.issn.1002-8331.2011.20.035]]]
- 8 C. Chen, J. Huang, and Y . Jiang, "Mining frequent items in uncertain dataset using compressed UF-tree," Application Research of Computers, vol. 31, no. 3, pp. 716-719, 2014. https://doi.org/10.3969/j.issn.10013695.2014.03.018doi:[[[10.3969/j.issn.10013695.2014.03.018]]]
- 9 Z. Li and J. Mo, "An improved data mining algorithm based on concept lattice," Journal of Chongqing Normal University (Natural Science Edition), vol. 30, no. 2, pp. 92-95, 2013. https://doi.org/10.11721/cqnuj20130221doi:[[[10.11721/cqnuj0221]]]
- 10 J. C. W . Lin, T. Li, M. Pirouz, J. Zhang, and P . Fournier-Viger, "High average-utility sequential pattern mining based on uncertain databases," Knowledge and Information Systems, vol. 62, pp. 1199-1228, 2020. https://doi.org/10.1007/s10115-019-01385-8doi:[[[10.1007/s10115-019-01385-8]]]
- 11 Y . Baek, U. Y un, E. Yoon, and P . Fournier-Viger, "Uncertainty-based pattern mining for maximizing profit of manufacturing plants with list structure," IEEE Transactions on Industrial Electronics, vol. 67, no. 11, pp. 9914-9926, 2020. https://doi.org/10.1109/TIE.2019.2956387doi:[[[10.1109/TIE.2019.2956387]]]
- 12 M. M. Rahman, C. F. Ahmed, and C. K. S. Leung, "Mining weighted frequent sequences in uncertain databases," Information Sciences, vol. 479, pp. 76-100, 2019. https://doi.org/10.1016/j.ins.2018.11.026doi:[[[10.1016/j.ins.2018.11.026]]]
- 13 G. Lee and U. Yun, "A new efficient approach for mining uncertain frequent patterns using minimum data structure without false positives," Future Generation Computer Systems, vol. 68, pp. 89-110, 2017. https://doi.org/10.1016/j.future.2016.09.007doi:[[[10.1016/j.future.2016.09.007]]]
- 14 G. Lee, U. Y un, and K. M. Lee, "Analysis of tree-based uncertain frequent pattern mining techniques without pattern losses," The Journal of Supercomputing, vol. 72, pp. 4296-4318, 2016. https://doi.org/10.1007/s11227-016-1847-zdoi:[[[10.1007/s11227-016-1847-z]]]
- 15 X. Zhao, D. Miao, and B. Q. Hu, "On relationship between three-way concept lattices," Information Sciences, vol. 538, pp. 396-414, 2020. https://doi.org/10.1016/j.ins.2020.06.007doi:[[[10.1016/j.ins.2020.06.007]]]
- 16 G. Liao, L. Wu, and C. Wan, "Frequent pattern mining of uncertain data streams based on probability decay window model," Journal of Computer Research and Development, vol. 49, no. 5, pp. 1105-1115, 2012.custom:[[[-]]]
- 17 S. Wang, G. Yang, and Z. Zhu, "Frequent item query algorithm based on uncertain data," Journal of Northeastern University (Natural Science Edition), vol. 32, no. 3, pp. 344-347, 2011. https://doi.org/10.3969/j.issn. 1005-3026.2011.03.010doi:[[[10.3969/j.issn.1005-3026.2011.03.010]]]
- 18 L. Zhang, H. Zhang, L. Yin, and D. Han, "Theory and algorithms of attribute decrement for concept lattice," Journal of Computer Research and Development, vol. 50, no. 2, pp. 248-259, 2013.custom:[[[https://crad.ict.ac.cn/en/article/id/721]]]