Chang Wang and Wen Zhang
Image Global K-SVD Variational Denoising Method Based on Wavelet Transform
Abstract: Many image edge details are easily lost in the image denoising process, and the smooth image regions are prone to produce jagged. In this paper, we propose a wavelet-based image global k- singular value decomposition variational method to remove image noise. A layer of wavelet decomposition is applied to the noisy image first. Then, the image global k-singular value decomposition (IGK-SVD) method is used to remove the random noise of low-frequency components. Furthermore, a constructed variational denoising method (VDM) removes the random noise in the high-frequency component. Finally, the denoised image is obtained by wavelet recon-struction. The experimental results show that the proposed method's peak signal-to-noise ratio (PSNR) value is higher than other methods, and its structural similarity (SSIM) value is closer to one, indicating that the proposed method can effectively suppress image noise while retaining more image edge details. The denoised image has better denoising effects.
Keywords: High Frequency , Image Global K-singular Value Decomposition (IGK-SVD) Method , Low Frequency , Variational Denoising Method (VDM) , Wavelet Decomposition
1. Introduction
Due to the existence of noise, the image's important information gets overwritten, which has an impact on the image's subsequent processing. Many scientists have spent a great deal of time and effort proposing many successful ways to overcome this problem, such as filtering-based, Fourier transformation, and wavelet thresholding methods. Although the above methods can achieve the purpose of noise suppression to a certain extent, there are some disadvantages at the same time. The filter-based method is simple, fast, and can effectively smooth the noise. However, the image edges are blurred to a certain extent, and some details may be removed [1,2] as noise points. These blurred points are removed because the Fourier transform method cannot be used in the time domain, and it is impossible to distinguish between noise and valuable high-frequency signals [3]. On the other hand, the wavelet method can cause image edge information loss, or the noise is not removed [4-9].
In recent years, image-denoising methods based on partial differential equations (PDEs) have become increasingly popular. One example is a classical total variational (TV) denoising model proposed [10] based on PDE theory, which can effectively preserve image edges. However, it is prone to staircase effects in smooth image regions. In order to avoid the above problems, an adaptive full variational model was proposed to introduce controllable filters into it [11]. Additionally, a regional spatial adaptive TV super-resolution technique was presented in the literature [12], thus achieving sound denoising effects.
Many scholars also proposed denoising models from the perspective of image features. For example, from analyzing non-local comparable properties of images, Chan's theory [13] presented a non-local mean (NLM) denoising method. Then, Gray theory [14], Monte Carlo theory [15], and fuzzy clustering theory [16] were introduced, respectively, to increase the NLM algorithm's denoising performance. A block matching and three-dimensional filtering (BM3D) technique was proposed based on non-local adaptive theory [17]. The algorithm was chosen as it has good edge retention capability. A sparse representation image denoising algorithm was proposed [18]. It can effectively construct a suitable dictionary from natural scenes and sparse representation of natural scenes and achieve an excellent denoising effect. However, the above algorithm relatively tends to lose the high-frequency signal of the image due to over-smoothing the noise, which leads to the denoising image blur.
Although the methods described above produced good results in image denoising, there are some limitations and challenges. (1) Regardless of the denoising method used, image details will be lost while removing noise, resulting in a blurred denoised image. (2) Many denoising images exhibit a jagged effect after removing image noise.
In order to address the issue of excessive image high-frequency signal loss and the denoised image's staircase effect, this paper proposes a global k-singular value decomposition (K-SVD) variational denoising method based on wavelet transform. First, the method decomposes the noisy image by wavelet technique, which can understand the noise distribution characteristics. Then the global K-SVD method denoises the low-frequency components. This method can successfully remove the noise and produce better visual denoised low-frequency components. The variational denoising approach reduces highfrequency component noise. Thus, resulting in the image retaining more high-frequency signals. Finally, wavelet reconstruction would be used to generate the denoised image.
This study makes two significant contributions. We propose a wavelet decomposition method, K-SVD, and a variational denoising algorithm to remove image noise. Then, a variational denoising model (VDM) is built to remove noise while preserving image edge details effectively.
2. Proposed Methodology
In order to remove the noise while avoiding the loss of image details and edge information, this paper uses wavelets to decompose the noisy image into one layer. The denoised image is decomposed into four images, the low-frequency component image and three high-frequency component images (horizontal high-frequency component, vertical high-frequency component, and diagonal method horizontal component). The low-frequency component represents the global information of the image. It does not include the high-frequency and edge detail information, so the global K-SVD method removes the lowfrequency component noise in this paper. While the high-frequency component mainly includes edge and detail information, if the global K-SVD method removes the noise of the high-frequency component, then the edge detail information will also be removed. Therefore, this paper studies a variable component denoising method with peer diffusion and anisotropic diffusion capability to solve this problem. This method removes the high-frequency component noise while the edge detail information is retained. The global method and the variational denoising method are described in detail below.
2.1 Image Global K-SVD Method
The expression for the image global K-SVD method is defined as [19]:
(1)
[TeX:] $$\left\{\hat{a}_{i j}, \hat{f}\right\}=\underset{a_{i j}, f}{\operatorname{argmin}} \lambda\|f-F\|_2^2+\sum_{i, j}\left\|D a_{i j}-A_{i j} \hat{f}\right\|_2^2+\sum_{i, j} \mu_{i j}\left\|a_{i j}\right\|_0,$$where the [TeX:] $$\underset{a_{i j}, f}{\operatorname{argmin}} \lambda\|f-F\|_2^2$$ is the fidelity term, is the first [TeX:] $$i j$$ approximate subgraph, [TeX:] $$A_{i j} f$$ is the first [TeX:] $$i j$$ sub-image, and [TeX:] $$R_{i j}$$ is the first [TeX:] $$i j$$ sub-image matrix, [TeX:] $$\sum_{i, j} \mu_{i j}\left\|a_{i j}\right\|_0$$ is the constraint term, where F is the noise image, f is the output image, [TeX:] $$\hat{a}_{i j}$$ is the sparse coefficients, D is the dictionary, and [TeX:] $$\lambda, \mu$$ is the penalty operator.
The [TeX:] $$\hat{a}_{i j}$$ Eq. (1) sum can be solved using a block coordinate minimisation algorithm. First, [TeX:] $$\hat{a}_{i j}$$ which is defined as
(2)
[TeX:] $$\hat{a}_{i j}=\underset{a_{i j}}{\operatorname{argmin}} \sum_{i, j}\left\|D a_{i j}-A_{i j} f\right\|_2^2+\sum_{i, j} \mu_{i j}\left\|a_{i j}\right\|_0 .$$The orthogonal matching tracking (OMP) is used to solve Eq. (2). the iteration stops when [TeX:] $$\left\|D a_{i j}-A_{i j} f\right\|_2^2\langle\varepsilon$$ satisfied, and the [TeX:] $$\hat{a}_{i j}$$ first [TeX:] $$i j$$ sub-image is obtained.
When all [TeX:] $$\hat{a}_{i j}$$ is solved, update f. Then [TeX:] $$\hat{f}$$ is calculated as
(3)
[TeX:] $$\hat{f}=\underset{f}{\operatorname{argmin}} \lambda\|f-F\|_2^2+\sum_{i, j}\left\|D a_{i j}-A_{i j} \hat{f}\right\|_2^2 .$$The approximate solution of Eq. (3) can be written as follows:
(4)
[TeX:] $$\hat{f}=\left(\lambda I+\sum_{i j} R_{i j}^T R_{i j}\right)^{-1}\left(\lambda F+\sum_{i j} R_{i j}^T D \hat{a}_{i j}\right).$$In Eq. (4), I is defined as the unit matrix.
2.2 Variational Denoising Method
The conventional TV method is easy to make the denoised image produce a staircase effect in the denoising process. A VDM based on anisotropic diffusion and homogeneous diffusion capability is proposed to solve the staircase effect, and this model is defined as follows:
(5)
[TeX:] $$\inf \left\{\left\{E(f)=\int_{\Omega}|\nabla f|^2\left(1+|\nabla f|^2\right)^{-\frac{1}{2}} d f+\lambda_0 \int_{\Omega}|f-F|^2 d f\right\}\right.,$$where the [TeX:] $$\int_{\Omega}|\nabla f|^2\left(1+|\nabla f|^2\right)^{-\frac{1}{2}} d f$$ is the regularization term and [TeX:] $$\lambda_0 \int_{\Omega}|f-F|^2 d f$$ is the fidelity the term, and [TeX:] $$\lambda_0$$ denotes the regularization parameter.
Eq. (5) is transformed into the Euler-Lagrange equation to calculate the extreme value of the energy generalization function. The Euler-Lagrange equation is defined as [20]:
(6)
[TeX:] $$F(D f, f, x, y)=|\nabla f|^2\left(1+|\nabla f|^2\right)^{-\frac{1}{2}}+\lambda_0|f-F|^2.$$To proceed, we now expand Eq. (6) in the following form:
(7)
[TeX:] $$F[D f, f, x, y]=2 \lambda_0(f-F)-\frac{\partial\left(\frac{2 f_x}{\sqrt{1+|\nabla f|^2}}-\frac{|\nabla f|^2\left(\frac{1}{|\nabla f|}+2\right) f x}{2\left(\sqrt{1+|\nabla f|^2}\right)^3}\right)}{\partial x}-\frac{\partial\left(\frac{2 f y}{\sqrt{1+|\nabla f|^2}}-\frac{|\nabla f|^2\left(\frac{1}{|\nabla f|}+2\right) f y}{2\left(\sqrt{1+|\nabla f|^2}\right)^3}\right)}{\partial y} .$$Eq. (7) can be discretized using the finite difference method, a spatial step 1 in the experiment. We propose the markers to portray the discrete derivatives in horizontal and vertical directions. [TeX:] $$D_{+x}, D_{-x}, D_{+y}, D_{-y}, D_{x 0}$$ set as the difference operator, the forward finite difference operator labelled with the plus sign (+) and the backward finite difference operator labelled with the minus sign (-), [TeX:] $$D_{x 0}, D_{y 0}$$ are the central difference operator.
Then
(8)
[TeX:] $$\begin{aligned} & \left(D_{ \pm x} f\right)_{i, j}= \pm\left(f_{i \pm 1, j}-f_{i, j}\right) / k \\ & \left(D_{ \pm y} f\right)_{i, j}= \pm\left(f_{i, j \pm 1}-f_{i, j}\right) / k \\ & \left(D_{x 0} f\right)_{i, j}=\left(f_{i+1, j}-f_{i-1, j}\right) / 2 k \\ & \left(D_{y 0} f\right)_{i, j}=\left(f_{i, j+1}-f_{i, j-1}\right) / 2 k. \end{aligned}$$The discretized form of Eq. (8) is defined as:
(9)
[TeX:] $$\begin{gathered} f_{i, j}=F_{i, j}+D_{-x}\left[D_{+x} f_{i, j} c_1\right]+D_{-y}\left[D_{+y} f_{i, j} c_3\right] \\ =F_{i, j}+\frac{1}{2 \lambda_0 k^2}\left[\left(f_{i+1, j}-f_{i, j}\right) c_1-\left(f_{i, j}-f_{i-1, j}\right) c_2\right]+\frac{1}{2 \lambda_0 k^2}\left[\left(f_{i, j+1}-f_{i, j}\right) c_3-\left(f_{i, j}-f_{i, j-1}\right) c_4\right], \end{gathered}$$where
For immobile points, the Gauss-Seidel iterative technique is used to solve Eq. (9).
(10)
[TeX:] $$\begin{aligned} f_{i, j}^{n+1}= & F_{i, j}+\frac{1}{2 \lambda_0 k^2}\left[\left(f_{i+1, j}^n-f_{i, j}^n\right) c_1-\left(f_{i, j}^n-f_{i-1, j}^n\right) c_2\right] \\ & +\frac{1}{2 \lambda_0 k^2}\left[\left(f_{i, j+1}^n-f_{i, j}^n\right) c_3-\left(f_{i, j}^n-f_{i, j-1}^n\right) c_4\right] . \end{aligned}$$Eq. (10) yields
3. Experimental Results
3.1 Image Global K-SVD Variational Denoising Process
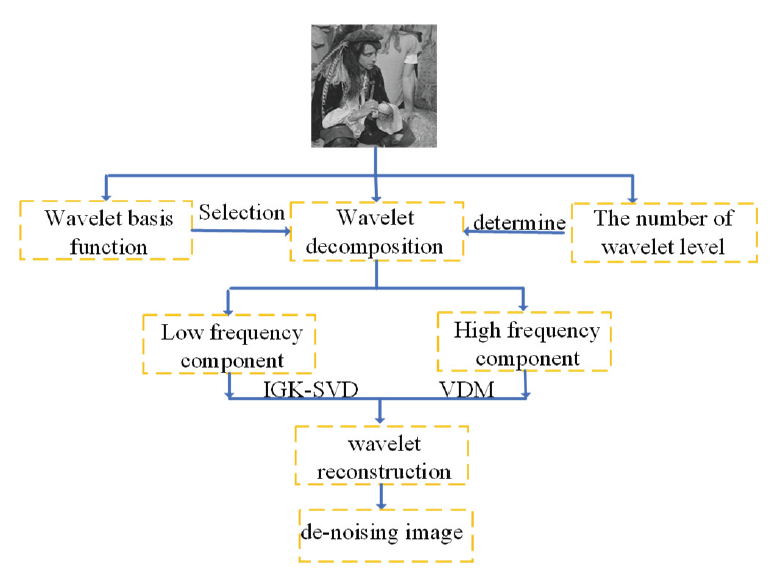
In order to solve the loss of more details in the image denoising process, this paper first uses a wavelet to decompose the noise image. Then the global K-SVD method is used to de-noise the low-frequency component. Followed by the constructed variational denoising method to remove the noise of the highfrequency component and, finally, the wavelet reconstruction method to generate the denoised image. The flowchart of the proposed method is shown in Fig. 1.
3.2 Random Noise Removal
3.2.1 Wavelet basis function selection and decomposition level determination
Based on the wavelet basis functions characteristics, wavelet basis functions are determined in this paper. Wavelet basis functions with support and orthogonality can be implemented quickly and have an excellent local time-frequency. When reconstructing signals, the wavelet basis functions smoothly and can avoid signal distortion. As a result, the wavelet basis function with the three characteristics mentioned above can be chosen. Therefore, the image-denoising evaluation index value primarily governs the number of wavelet levels.
3.2.2 Random noise removal
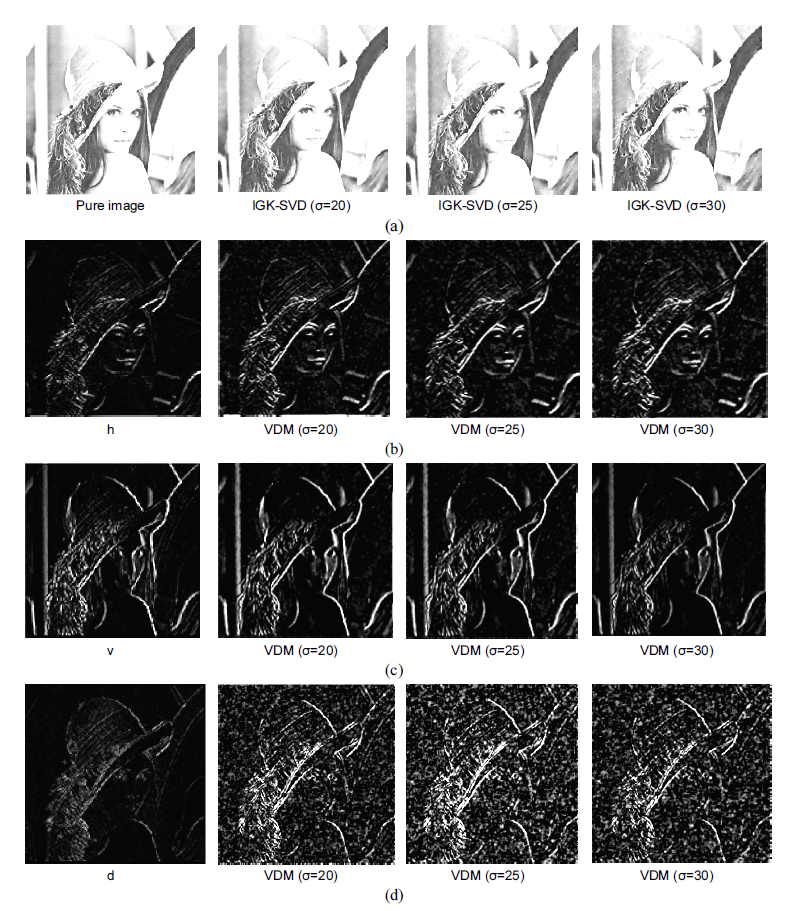
In this paper, an image with apparent texture features is selected as the experimental image and random noise whose noise standard deviation of 20, 25 and 30 is added to this image. The size of the experimental image is 256 × 256 pixel. Experimenting with a wavelet decomposition level on a noisy image can yield the optimal evaluation index value of denoising. Decomposed from the pure image are the lowand high-frequency components in the horizontal direction, the high-frequency component in the vertical direction, and the high-frequency component in the diagonal direction. In Fig. 2, these images are represented by the letters a, h, v, and d. de-a, de-h, de-v, and de-d, on the other hand, represent low- and high-frequency components decomposed from the noise image in the horizontal direction, high-frequency components decomposed in the vertical direction, and high-frequency components decomposed in the diagonal direction.
From Fig. 2(a), the high-frequency components obtained by the one-layer decomposition of the Haar wavelet basis function can better preserve image edge detail information. From Fig. 2(b)–2(d), it can be seen that the noisy images are contaminated by random noise in both low-frequency components and high-frequency components after wavelet decomposition. In the horizontal and vertical high-frequency components, the edge detail information of the image can be seen. In contrast, the image edge detail information in the diagonal high-frequency components is buried in the noise. While making the denoised image present a better visual effect, we ensured that the IGK-SVD and VDM methods reduced noise efficiently. Such a reassurance was done to prevent the destruction of useful high-frequency information as much as possible. This step was taken to remove the noise in the low- and high-frequency components; the results of the denoising step are shown in Fig. 3.
Fig. 2.

The VDM method is used to denoise the image, as shown in Fig. 3. The random noise in the highfrequency component is effectively removed, but different image edge details are preserved. Image edge details in the high-frequency component along the horizontal and vertical directions can be preserved, while some details are removed as noise points. Because the high-frequency component along the diagonal direction contains much noise, the image edge detail information is limited. The regularization intensity of the VDM model is increased to effectively remove noise, resulting in more detail points being removed as noise points. Furthermore, after de-noising with the IGK-SVD method, we found that the random noise is effectively suppressed, and the denoised low-frequency components have a better visual effect.
Fig. 3.

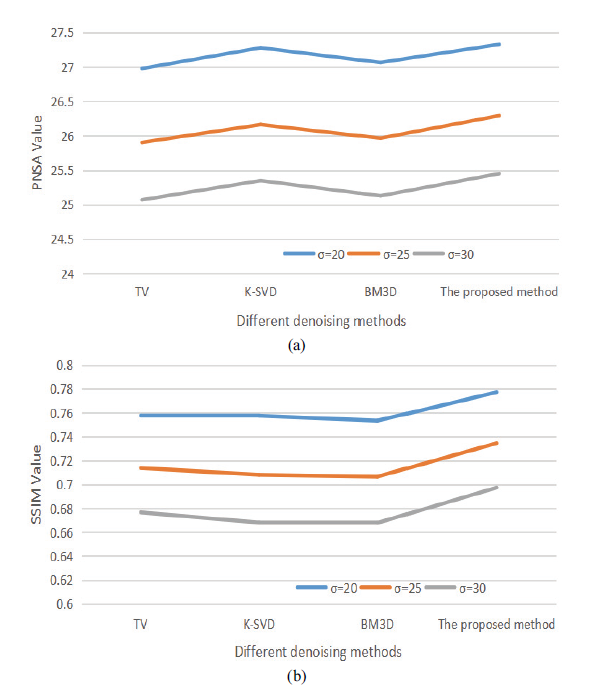
The high-frequency and low-frequency denoised components are rebuilt to produce the denoised pictures. Moreover, the performance of the estimation method developed in this paper compared with the TV model [10], BM3D model, which is currently recognized to have a better denoising effect [17], KSVD model [18] and Raghav's method [21]; Fig. 4 depicts the experimental results.
The comparison and method developed in this paper can effectively suppress random noise, as shown in Fig. 4. However, the denoising effect is different—denoised using the TV method ( =20, 25, 30 is especially obvious). The image has a better visual effect after denoising with K-SVD and BM3D. However, it is suggested that the two methods described above focus on smoothing random noise, resulting in a loss of image edge details. According to the enlarged images, loss of edge detail may result in blurring denoised images. The experimental results show that using the approach presented in this study, not only can random noise be efficiently removed, but more image edge details can be preserved, and the denoising image has a superior visual impression. In addition to the visual effect of denoised pictures, two evaluation indexes are employed to evaluate the denoising effect: structural similarity (SSIM) and peak signal-to-noise ratio (PSNR). The experimental findings are shown in Table 1.
Fig. 4.

Table 1.
| Method | /PSNR | SSIM | ||||
|---|---|---|---|---|---|---|
| 20/22.1182 | 25/20.1800 | 30/18.5964 | =20 | =25 | =30 | |
| TV | 26.9777 | 25.9039 | 25.0694 | 0.7575 | 0.7137 | 0.6765 |
| K-SVD | 27.2776 | 26.1625 | 25.3488 | 0.7574 | 0.7080 | 0.6681 |
| BM3D | 27.0646 | 25.9662 | 25.1284 | 0.7533 | 0.7065 | 0.6678 |
| Proposed method | 27.3271 | 26.2920 | 25.4504 | 0.7771 | 0.7345 | 0.6973 |
It can be seen that the TV method's PNSR values are statistically lower than those of the K-SVD and BM3D methods, but the SSIM values are higher than those of these two methods, as shown in Fig. 5(a), 5(b) and Table 1. It indicates that the TV method can retain more detailed image edge information, but the denoising effect is poor. In contrast, the K-SVD method and BM3D method have better denoising effects but at the cost of losing more detailed information about the image edge (as shown in Fig. 4). The suggested method's PSNR and SSIM values are greater than those of the TV, BM3D, and K-SVD methods, as shown in Fig. 5(a), 5(b) and Table 1. The suggested strategy can reduce picture random noise while retaining more precise image edge information.
Fig. 5.
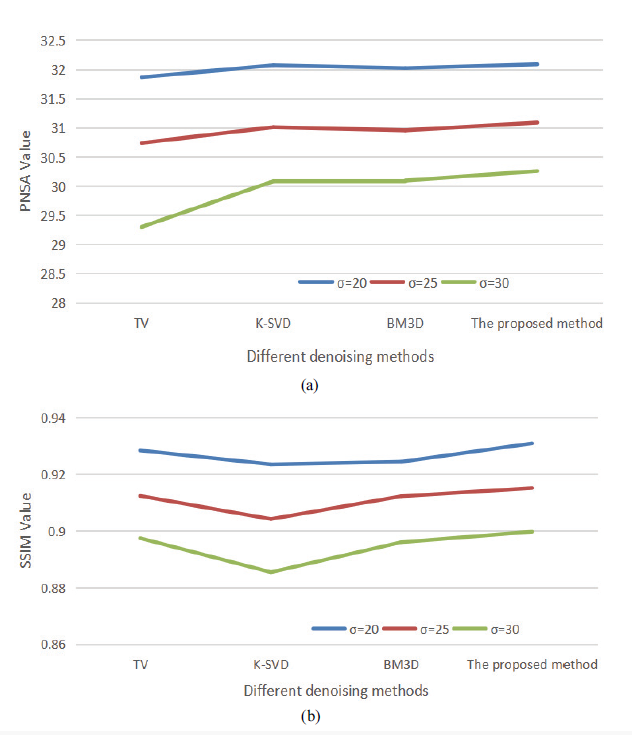
In order to ensure that the proposed method is stable, another image (the size of the image is 256 × 256 pixel) is selected for denoising, and the experimental results and image denoising evaluation indexes are shown in Figs. 6, 7 and Table 2.
The model constructed in this paper can effectively remove noise based on the results of Figs. 6, 7 and Table 2. Fig. 8 compared with the TV, K-SVD, and BM3D methods. Furthermore, more detailed information on the image edge can be preserved.
Table 2.
| Method | /PSNR | SSIM | ||||
|---|---|---|---|---|---|---|
| 20/22.0852 | 25/20.1470 | 30/18.5633 | =20 | =25 | =30 | |
| TV | 31.8650 | 30.7371 | 29.2978 | 0.9284 | 0.9123 | 0.8974 |
| K-SVD | 32.0718 | 31.0102 | 30.0819 | 0.9235 | 0.9042 | 0.8854 |
| BM3D | 32.0210 | 30.9553 | 30.0921 | 0.9244 | 0.9122 | 0.8960 |
| Proposed method | 32.0891 | 31.0889 | 30.2575 | 0.9309 | 0.9151 | 0.8997 |
5. Conclusion
This study proposes a wavelet-based IGK-SVD-VDM denoising method that preserves more image edge details. The simulation experiments demonstrate that the new method effectively denoises random noise while retaining more detailed information on the image edge. Furthermore, the denoising image makes a better visual impression.
Although the proposed method has a good denoising effect, it has some drawbacks. It is easy to lose details when using the constructed variational denoising method to remove high-frequency components, especially those decomposed in the diagonal direction.
Acknowledgement
This research was supported by the Fund project of the Provincial Education Department (No. LJKMZ20220638) and the Open Fund Project of the Marine Information Technology Innovation Center of the Ministry of Natural Resources. We appreciate the time and thought given by the anonymous reviewers who diligently reviewed this letter and gave valuable feedback.
References
- 1 D. Singh and A. Kaur, "Fuzzy based fast non local mean filter to denoise Rician noise," Materials Today: Proceedings, vol. 46(Part 15), pp. 6445-6452, 2021.doi:[[[10.1016/j.matpr.2021.03.494]]]
- 2 D. Singh and A. Kaur, "Improved fuzzy based non-local mean filter to denoise Rician noise," Turkish Journal of Computer and Mathematics Education (TURCOMAT), vol. 12, no. 7, pp. 2116-2121, 2021.doi:[[[10.17762/turcomat.v12i7.3352]]]
- 3 M. F. Wahab, F. Gritti, and T. C. O'Haver, "Discrete Fourier transform techniques for noise reduction and digital enhancement of analytical signals," TrAC Trends in Analytical Chemistry, vol. 143, article no. 116354, 2021. https://doi.org/10.1016/j.trac.2021.116354doi:[[[10.1016/j.trac..116354]]]
- 4 W. Q. Fan, W. S. Xiao, and W. S. Xiao, "Image denoising based on wavelet thresholding and Wiener filtering in the wavelet domain," The Journal of Engineering, vol. 2019, no. 19, pp. 6012-6015, 2019.doi:[[[10.1049/joe.2019.0194]]]
- 5 J. Tang, S. Zhou, and C. Pan, "A denoising algorithm for partial discharge measurement based on the combination of wavelet threshold and total variation theory," IEEE Transactions on Instrumentation and Measurement, vol. 69, no. 6, pp. 3428-3441, 2020.doi:[[[10.1109/tim.2019.2938905]]]
- 6 M. Aamir, Z. Rahman, Y . F. Pu, W. A. Abro, and K. Gulzar, "Satellite image enhancement using waveletdomain based on singular value decomposition," International Journal of Advanced Computer Science and Applications, vol. 10, no. 6, pp. 514-519, 2019.doi:[[[10.14569/IJACSA.2019.0100667]]]
- 7 Z. Rahman, Y . F. Pu, M. Aamir, and S. Wali, "Structure revealing of low-light images using wavelet transform based on fractional-order denoising and multiscale decomposition," The Visual Computer, vol. 37, pp. 865880, 2021.doi:[[[10.1007/s00371-020-01838-0]]]
- 8 B. Ullah, A. Khan, M. Fahad, M. Alam, A. Noor, U. Saleem, and M. Kamran, "A novel approach to enhance dual-energy X-ray images using region of interest and discrete wavelet transform," Journal of Information Processing Systems, vol. 18, no. 3, pp. 319-331, 2022.doi:[[[10.3745/JIPS.01.0086]]]
- 9 R. Kayalvizhi, S. Malarvizhi, A. Topkar, and P . Vijayakumar, "Raw data processing techniques for material classification of objects in dual energy X-ray baggage inspection systems," Radiation Physics and Chemistry, vol. 193, article no. 109512, 2022. https://doi.org/10.1016/j.radphyschem.2021.109512doi:[[[10.1016/j.radphyschem..109512]]]
- 10 L. I. Rudin, S. Osher, and E. Fatemi, "Nonlinear total variation based noise removal algorithms," Physica D: Nonlinear Phenomena, vol. 60, no. 1-4, pp. 259-268, 1992.doi:[[[10.1016/0167-2789(92)90242-f]]]
- 11 W. Zhang, Y . Cao, R. Zhang, and Y . Wang, "Image denoising using total variation model guided by steerable filter," Mathematical Problems in Engineering, vol. 2014, article no. 423761, 2014. https://doi.org/10.1155 /2014/423761doi:[[[10.1155//423761]]]
- 12 C. Liu, H. Zou, C. Li, Y . Liu, Y . Wang, S. Jia, and S. Zhou, "An adaptive texture-preserved image denoising model," Journal of Ambient Intelligence and Humanized Computing, vol. 6, pp. 689-697, 2015.doi:[[[10.1007/s12652-015-0286-7]]]
- 13 A. Buades, B. Coll, and J. M. Morel, "A review of image denoising algorithms, with a new one," Multiscale Modeling & Simulation, vol. 4, no. 2, pp. 490-530, 2005.doi:[[[10.1137/040616024]]]
- 14 H. Li and C. Y . Suen, "A novel non-local means image denoising method based on grey theory," Pattern Recognition, vol. 49, pp. 237-248, 2016.doi:[[[10.1016/j.patcog.2015.05.028]]]
- 15 S. H. Chan, T. Zickler, and Y . M. Lu, "Monte Carlo non-local means: random sampling for large-scale image filtering," IEEE Transactions on Image Processing, vol. 23, no. 8, pp. 3711-3725, 2014.doi:[[[10.1109/tip.2014.2327813]]]
- 16 B. Liu, X. Sang, S. Xing, and B. Wang, "Noise suppression in brain magnetic resonance imaging based on non-local means filter and fuzzy cluster," Optik, vol. 126, no. 21, pp. 2955-2959, 2015.doi:[[[10.1016/j.ijleo.2015.07.056]]]
- 17 K. Dabov, A. Foi, V . Katkovnik, and K. Egiazarian, "Image denoising by sparse 3-D transform-domain collaborative filtering," IEEE Transactions on Image Processing, vol. 16, no. 8, pp. 2080-2095, 2007.doi:[[[10.1109/tip.2007.901238]]]
- 18 M. Aharon, M. Elad, and A. Bruckstein, "K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation," IEEE Transactions on Signal Processing, vol. 54, no. 11, pp. 4311-4322, 2006.doi:[[[10.1109/TSP.2006.881199]]]
- 19 M. Lebrun and A. Leclaire, "An implementation and detailed analysis of the K-SVD image denoising algorithm," Image Processing On Line, vol. 2, pp. 96-133, 2012.doi:[[[10.5201/ipol.2012.llm-ksvd]]]
- 20 C. Wang, Y . Zhang, X. Wang, and S. Ji, "Research on destriping method in vertical direction for Landsat image," Journal of Huazhong University of Science and Technology (Natural Science Edition), vol. 4, no. 4, pp. 121-126+132, 2019.custom:[[[-]]]
- 21 K. Bnou, S. Raghay, and A. Hakim, "A wavelet denoising approach based on unsupervised learning model," EURASIP Journal on Advances in Signal Processing, vol. 2020, article no. 36, 2020. https://doi.org/10.1186/ s13634-020-00693-4doi:[[[10.1186/s13634-020-00693-4]]]