Intelligent Detection Algorithm for Fall from Height Based on Support Vector Machines

1. Introduction

In the construction industry, falls from heights are the most frequent and dangerous accidents. Consequently, the reduction and prevention of such incidents is crucial for safe operations. In the context of the rapid evolution of computational and sensor technologies, the inception of an algorithm that facilitates the precise detection and prompt notification of high-altitude worker fall incidents is of paramount significance and bears substantial implications for practical application.

Currently, fall detection algorithms primarily utilize two methods: video image analysis and acceleration analysis. The video image analysis method [1,2] involves cameras to capture the motion of the human body. Image processing algorithms are then used to analyze the positional changes in the body's joints to identify characteristic movements associated with a fall and determine if a fall event has occurred. Xi et al. [3] proposed a method that extracts static characteristics, such as aspect ratio and tilt angle, from video frames to determine the motion state of a character. This approach reduces computational complexity and improves accuracy. However, the image-based method comes with limitations, as it requires a fixed camera position, which restricts detection to a specific area, and raises privacy concerns for individuals being monitored. Given that work at height typically takes place in outdoor construction environments, where the activity area is not fixed. Therefore, video image analysis proves unsuitable for this scenario. Another approach is the acceleration-based analysis method, which analyzes the acceleration characteristics of the human body in different motion states for fall detection. In this field, two popular research methods for fall detection are the threshold method and artificial intelligence-based algorithms. The threshold method determines fall occurrences by comparing extracted features with pre-defined thresholds but suffers from limitations in accuracy and reliability due to reliance on experimental data or personal experience. In contrast, artificial intelligence algorithms leverage AI techniques to improve fall detection. For instance, Leone et al. [4] used a three-axis acceleration sensor to collect data, analyze motion characteristics, and achieve 98% accuracy in categorizing four human postures. Recent research further advances this field. Yhdego et al. [5] conducted a feasibility study on real-time, robust fall detection using wearable sensors and deep learning methods, Sengul et al. [6] reviewed deep learning-based systems for fall detection, and Zhang et al. [7] explored machine learning-based edge computing for real-time fall detection. These studies represent significant progress in developing adaptive, robust fall detection systems that address the complexities and limitations of traditional methods, reduce latency, and enhance system efficiency in dynamic environments. Intelligent algorithms based on support vector machines (SVM) can effectively characterize observed objects using fewer features [8].

This structure of the paper is organized as follows: Section 2 describes the proposed fall detection algorithm based on SVM, including data preprocessing, feature selection, and model construction. In Section 3, we design and develop the transmitter model based on this algorithm and conduct an analysis and comparison with existing solutions. Section 4 concludes this paper.

2. Intelligent Fall Detection Algorithm

2.1 Data Preprocessing

The SVM is a supervised learning algorithm employed for binary and multicategory classification tasks. Its primary objective is to determine the optimal hyperplane that effectively distinguishes samples belonging to distinct classes. SVM enhances model robustness through kernel functions to enable nonlinear mapping and classification. Furthermore, it exhibits superior generalization capabilities, even with a limited number of training samples. As a result, it proves well-suited for addressing challenges associated with small-sample datasets.

In this study, the Hilbert transform is applied to the original data to extract the vibration envelope, which represents the upper and lower boundaries of the vibration signal derived from the original acceleration signal. This step is crucial for fall detection, as fall events often exhibit distinctive vibration signals. Through the Hilbert transform and the calculation of the acceleration envelope [9], high-frequency noises and interferences can be effectively filtered out, with a cleaner and smoother vibration envelope curve obtained.

The Hilbert transform method is utilized to find the envelope of the filtered signal x(t), and the computational flow of the Hilbert transform [TeX:] $$\widehat{H}(t)$$ of the signal x(t) is shown in Eq. (1):

where * is the convolution symbol, and the analytic signal w(t) of the signal x(t) is defined in Eq. (2):

This yields the envelope value A(t) of the signal x(t) as in Eq. (3):

Take the acceleration over time data and perform the Hilbert transform as described above to obtain the data after filtering.

In this paper, the following four eigenvalues are extracted based on the original acceleration data. The duration of the weightlessness phase of the human body is 0.3–0.5 seconds, and the window time T is set to 0.5 seconds in this system.

1) The cumulative rate of change of the combined acceleration, ACC, refers to the vector sum of the three axial acceleration components, reflecting the integrated average of the body's acceleration over a cycle. It is defined in Eq. (4):

where [TeX:] $$a_x, a_y, \text { and } a_z$$ are the triaxial accelerations.

2) The change in amplitude of acceleration, denoted as RS, is the cumulative amount of change in three-axis acceleration, indicating the intensity of acceleration. A larger amplitude of acceleration usually suggests that the object is undergoing rapid motion, whereas a smaller one may indicate that the object is at a standstill or in a slow-moving state. This is defined in Eq. (5):

3) The rate of change in the magnitude of acceleration (RST) is calculated using Eq. (5). This calculation is performed to detect changes in the amplitude of acceleration. Monitoring the rate of change in the amplitude of acceleration enables the determination of whether the object has undergone a rapid and intense movement within a short period. This condition is defined in Eq. (6):

4) For the acceleration displacement change (ACD), the change displacement of acceleration provides information about the change in the position of the object in fall detection. The change displacement, calculated by monitoring the integration of acceleration over time, can be used to determine the presence of a significant change in the motion state of the object. The calculation process is as follows:

First, obtain the velocity values [TeX:] $$V_x, V_y, V_z$$ in three directions, as defined in Eq. (7):

The combined acceleration change displacement is then defined in Eq. (8):

2.2 Support Vector Machine Fall Detection Algorithm

The core tenet of the SVM for addressing classification challenges is centered on pinpointing a hyperplane within the feature space that optimizes the demarcation between distinct classes of data. In scenarios where sensor-collected sample data presents itself as linearly indistinguishable, the SVM algorithm employs a Gaussian kernel function, known colloquially as the radial basis function (RBF), to facilitate the necessary transformation. This kernel function excels in nonlinear mapping and offers a high degree of parameter tunability, which is indispensable for the nuanced analysis of complex sensor data. The adjustable parameter σ within the Gaussian kernel endows the model with the agility to respond to a spectrum of data features, thereby refining the model's complexity and tailoring it to specialized tasks, such as the detection of falls from elevated heights. The positive definite attribute of the Gaussian kernel is instrumental in securing a globally optimal solution, a pivotal aspect that underpins the model's stability and reliability. The efficacy of the RBF kernel is further corroborated by its ubiquitous application in the domain of pattern recognition, where it has demonstrated its performance in managing intricate classification tasks with precision.

The expression for the hyperplane is given in Eq. (9):

where x is the feature vector of the training sample, w is the coefficient vector of the classification hyperplane in the feature space, and b is the threshold of the classification surface. To maximize the classification interval, it is reformulated as an equivalent optimization problem in Eq. (10):

3. Experimental Results and Analysis

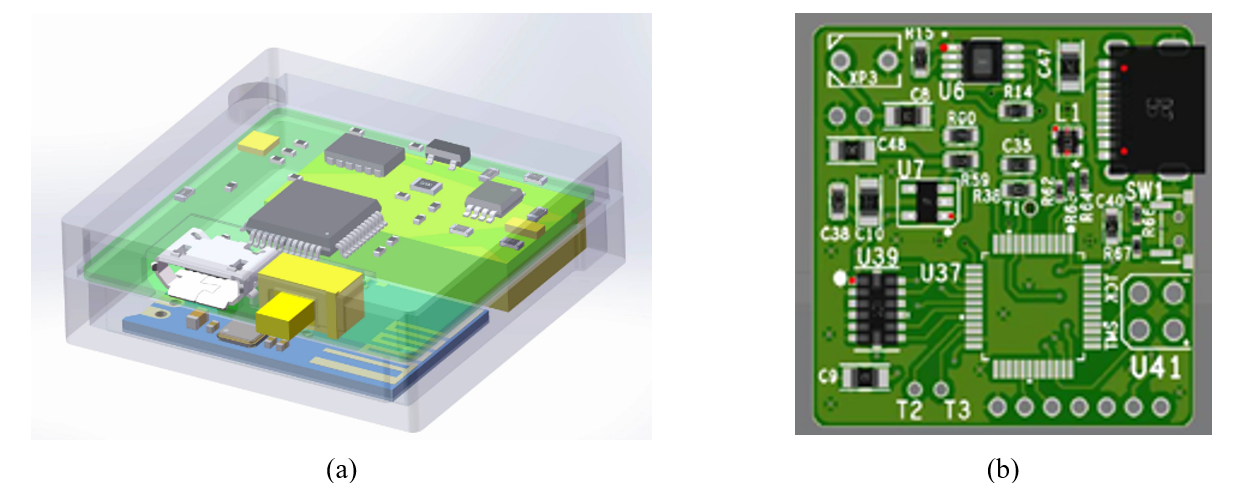
The experimental high-altitude fall intelligent detection system is designed with the primary function as a signal transmitter. The accelerometer module utilizes the MPU6050 accelerometer sensor, which measures acceleration in three directions. The high-altitude fall detection module employs the STM32F103 microcontroller responsible for the fall detection functionality. Real-time acceleration data is fed into a trained SVM model for classification. Upon the detection of a falling event, the system activates the signal transmission module to send out a signal. The internal and circuit diagrams of the transmitter are visually presented in Fig. 1.

In the experiment, the acceleration sensor is set to collect three-axis acceleration information at a sampling frequency of 30 Hz. The dataset includes daily behaviors such as walking and simulated falls. The choice is influenced by relatively subdued human activities in the high-construction environment. Four experimenters from three different age groups—young (18–30 years), middle-aged (31–50 years), and older adults (51+ years)—with two males and two females in each group, contributed to the collection of 6,000 data samples. After preprocessing, the dataset was balanced to include 3,000 fall detection samples. Of these, 2,000 samples are used for training the model, while the remaining 1,000 samples are allocated to the test set for evaluation. Both sets include two categories: normal and fall. Each sample extracts four eigenvalues that together form the eigenvectors ACC, RS, RST, and ACD. Due to the linear indivisibility of the sample data, the SVM initiates computation in the low-dimensional space, followed by the use of a kernel function to map inputs into a high-dimensional eigenspace. The SVM then constructs optimal separating planes in the high-dimensional space to realize the nonlinear classification of the data. The procedure involves the obtained acceleration feature data to continuously train the iterative classifier and complete the fall detection classifier training.

In this genetic algorithm optimization process, the fitness curve illustrates the performance variations across 100 generations. Through this evolutionary approach, we identified the optimal penalty factor C = 0.62 and RBF parameter γ = 37.4, which strike an ideal balance between classification accuracy and computational efficiency. This parameter combination enhances model performance by maintaining high accuracy while minimizing the computational load.

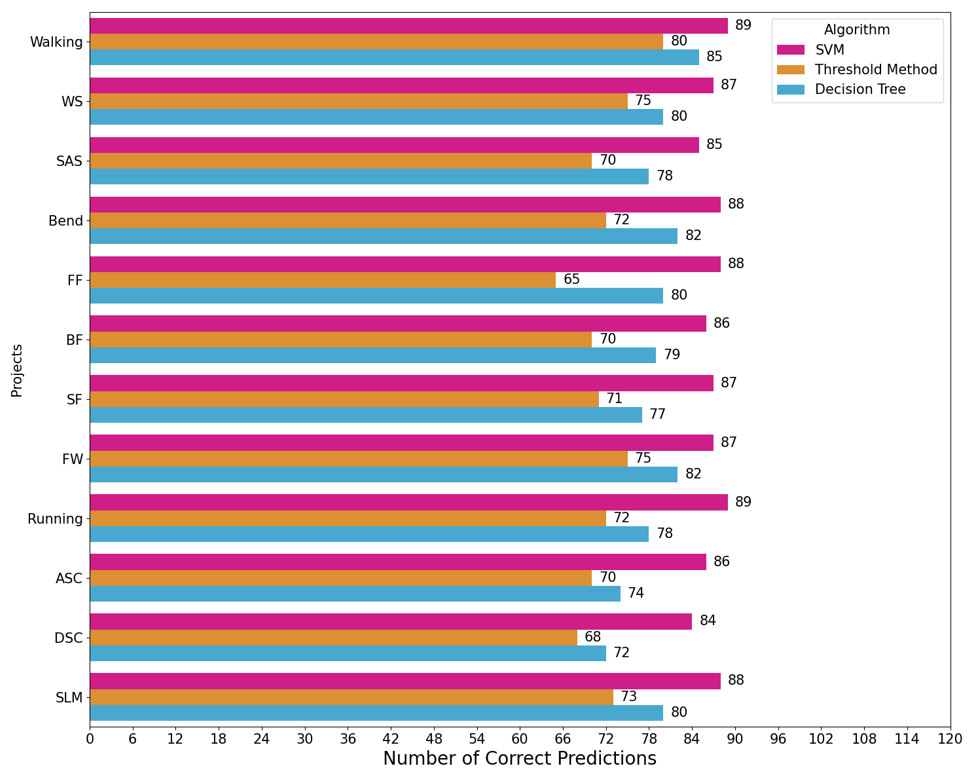
To assess the performance of the proposed classification algorithm, a dataset comprising 1,080 randomly selected samples was utilized, which included 270 fall event samples and 810 samples of daily activities. The predictive performance of three algorithms under varying operational conditions was examined: the proposed classification algorithm, a traditional threshold-based algorithm, and a decision tree-based algorithm. The related results are illustrated in Fig. 2. The performance metrics for the threshold method were derived from an empirical study by Cao et al. [10]. The decision tree classifier was configured with a maximum depth of 10, and a minimum sample size of 20 was required to split nodes.

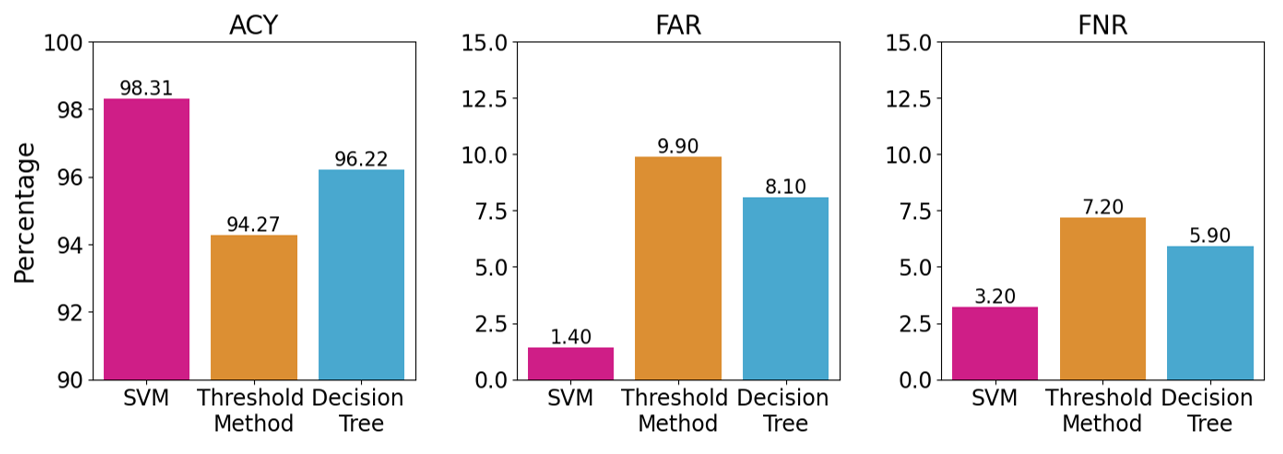
WS represents slow walking, SAS refers to the transition from sitting to standing, SAF simulates the fall process, FW stands for fast walking, ASC represents ascending stairs, DSC represents descending stairs, SLM refers to sideways movement, and Running represents the running activity. For each non-fall daily activity, 90 samples have been collected. Additionally, three types of falls—forward falls (FF), backward falls (BF), and sideways falls (SF)—have been included in the dataset, with 90 samples collected for each fall scenario. The graph above illustrates the number of correctly predicted activities by various algorithms. In evaluating fall detection algorithms, relying only on a single accuracy metric is inadequate. This limitation arises from persistent problems such as misclassification, where normal activities are erroneously identified as falls, and underclassification, where actual falls are not detected. To thoroughly assess the performance of these algorithms, a combination of three critical metrics is employed: accuracy (ACY), false alarm rate (FAR), and false negative rate (FNR). These metrics are derived from four distinct outcomes: true positives (TP) for accurate fall detections, false positives (FP) for the misclassification of daily activities as falls, true negatives (TN) for the correct identification of non-fall activities, and false negatives (FN) for instances where a fall is incorrectly categorized as a regular behavior. The ACY is quantified by the formula (TP + TN) / (TP + FP + TN + FN), which represents the proportion of correct identifications of falls and non-falls among all cases, thus reflecting the algorithm's overall effectiveness. The FAR is calculated as FP / (FP + TN), indicating the frequency at which the algorithm erroneously flags non-fall activities as falls. Conversely, the FNR is given by FN / (TP + FN), highlighting the proportion of actual falls that the algorithm fails to detect. The ACY, FAR, and FNR results for the three algorithms are presented in Fig. 3.

The SVM algorithm, while demonstrating a lower recognition accuracy for daily activities such as regular walking, small steps, and slow walking compared to the threshold-based method, excels in environments with complex activity patterns due to its ability to integrate a broader range of features. This complexity makes it superior in scenarios where nuanced differentiation of activities is crucial. In contrast, the threshold-based method, relying on a single criterion, often fails to accurately capture everyday activities, which do not exceed the predefined threshold, leading to frequent misclassifications. However, it tends to exhibit a higher rate of misjudgment for activities involving bending, falling, and other rapid acceleration changes. The SVM algorithm, by leveraging its sophisticated feature analysis, yields more accurate results in these challenging conditions. The Decision Tree algorithm shows robust performance in detecting daily activities with lower false alarm and false negative rates. Particularly in projects such as Bend and SAF, while the Decision Tree algorithm outperforms the threshold method, it remains close to or slightly below the SVM algorithm in effectiveness, thus highlighting the advantages of SVM in recognizing rapid motion changes.

4. Conclusion

The fall detection problem addressed in this paper is fundamentally a binary decision problem. We have constructed a human fall detection model using the SVM method. Extensive simulated fall experiments and parameter adjustments demonstrate that the trained model exhibits high reliability and accuracy in classifying normal and fall activities. Compared to traditional threshold methods, the model achieves higher precision, enhancing the system's usability in fall detection. Currently, we have already expanded the dataset to include more daily activities and fall scenarios, which helps improve the model's robustness and generalization capabilities. However, we acknowledge the limitations due to the reliance on simulated fall data in a laboratory setting, which may differ from human falls in actual work settings. To address this issue, future research will focus on collecting real-world fall data through collaborations with healthcare institutions or using wearable technology in everyday life. Further expanding the dataset will contribute to developing a more comprehensive model. Additionally, integrating sensors such as accelerometers, gyroscopes, and pressure sensors, along with exploring advanced machine learning techniques like deep learning and ensemble methods, will help improve detection accuracy and reliability.