Huifang Shan , Junrui Han and Zhanfang Li
Construction of Formative Evaluation System in Business English Listening and Speaking Course Using Fuzzy Hierarchy Analysis Process
Abstract: The classroom learning process is multi-dimensional and comprehensive, and formative evaluation is the key way to measure its effectiveness. When conducting the evaluation, teachers need to comprehensively examine the diverse performance of students and carefully establish evaluation criteria to ensure an objective and fair assessment of the learning behavior. This not only aids in testing the teaching effect but also provides robust support for the continuous improvement of classroom instruction. This study applies the fuzzy analytic hierarchy process to thoroughly analyze each aspect of the Business English Listening and Speaking Course, establish the logical relationship between formative elements, and subsequently construct an evaluation matrix. Simultaneously, the paper employs fuzzy theory to quantify the evaluation process, making it more precise and operational, and thereby produces a model for the formative evaluation system. Through comprehensive analysis and interpretation of the evaluation results, a more scientific and equitable evaluation of students’ learning processes is achieved.
Keywords: Business English Listening and Speaking Course , Formative Evaluation , FAHP , System Model
1. Introduction
Apart from applying appropriate teaching theories and effective teaching methods, teachers should use evaluation methods accurately to objectively evaluate students in order to achieve the best teaching effect. Formative evaluation can help teachers track students’ progress in knowledge and learning effectiveness, enabling timely teaching plan adjustments and method improvements. However, the commonly adopted impression-based evaluation and the oversimplified use of activity average scores, which fail to reflect objectivity, accuracy, and fairness, cannot provide constructive feedback and effective guidance in teaching.
Taking the Business English Listening and Speaking Course as an example, this paper applies the fuzzy analytic hierarchy process (FAHP) to enhance the objectivity and fairness of formative evaluation. This course’s practical nature demands diverse and task-based activities, posing a challenge to objective evaluation. Teachers’ accurate and fair judgments of students’ performance in activities can motivate students’ enthusiasm, which is conducive to guiding teaching practice and improving teaching quality. FAHP quantifies fuzzy decisions and provides auxiliary decision-making support for formative evaluation in the Business English Listening and Speaking Courses in higher education.
2. Formative Evaluation Analysis of the Business English Listening and Speaking Course
2.1 Significance of Formative Evaluation
Compared with traditional summative evaluation, formative evaluation focuses on students’ learning effectiveness. It aims to motivate independent learning, guide processes, enhance achievement and confidence, and foster teamwork, thereby transforming students from passive recipients to active participants in evaluation.
This process evaluation is an informal sustainable evaluation conducted in an open environment. It focuses on the students’ learning process, evaluating not only their knowledge and skills but also non-quantifiable dimensions such as learning interests, learning strategies, learning attitudes, participation awareness, cooperative spirit, and cultural consciousness [1]. The evaluation, which continuously gathers teaching information and provides feedback during the teaching process, is an important component and driving factor of teaching, thus becoming a systematic evaluation to improve teaching.
This kind of evaluation is also an important guarantee to achieve the curriculum objectives. Its proper application in the Business English Listening and Speaking Course can effectively compensate for some deficiencies in the current teaching and the final testing. The pure summative evaluation that overlooks the learning process of students’ listening and speaking, fails to comprehensively measure their learning effectiveness and detect their mastery of knowledge and skills in real time, which will gradually diminish students’ enthusiasm for learning [2].
2.2 Design of Formative Evaluation Activities for the Course
Formative evaluation is not solely based on teachers’ evaluation needs, but prioritizes students’ learning needs. It emphasizes the process and experience of students in learning, highlights the interaction of multiple factors in the evaluation process, and attaches great importance to teacher-student communication. When designing evaluation activities, teachers should consider students’ ongoing performance, achievements, emotions, and attitudes. These activities aim to stimulate learning interest, enhance English communication skills, and cultivate listening, speaking, thinking, and communication abilities. Formative evaluation helps students regulate their learning, achieve a sense of accomplishment, and boost self-confidence. Based on these features, professional objectives, and curriculum requirements, the design standards for the course formative evaluation are as follows:
The first is the integration of in-class and out-of-class learning. Language learning involves multiple applications and practices, not only within the limited class time, but also in the boundless extension outside class. Students should be encouraged to speak and listen to English more often outside class.
The second is to assess learning attitudes and habits through a combination of self, peer, and teacher evaluations. As the focal point, students should engage in self-evaluation and participate in peer valuations focusing on “practice processes,” like cooperation spirit, inquiry ability and communication skills. Then students are guided to seriously reflect on the evaluation results and fully recognize their own quality development, thus which plays the guiding and motivational role of evaluation.
The third is the combination of online and offline activities. This involves fully utilizing online resources and the school’s learning platform to establish student-centered teaching activities. The application of computer networks and multimedia technology makes teaching activities unrestricted by space and time. Consequently, with the convenient online activities, language usage can also be extended beyond the class.
Based on these considerations, teachers design eight formative evaluation activities every semester for the university course. Given the complexity of evaluating processes vs. outcomes, and students’ varying theoretical knowledge and judgment standards, self and peer evaluations may not always be scientific. Non-quantitative elements like learning interest and strategies are hard to quantify, which demands more time and effort from teachers. To address the issues arising during the evaluation process, this study employs FAHP to create an evaluation model.
3. Fuzzy Analytic Hierarchy Process
3.1 Construction of a Hierarchical Structure Model
The analytic hierarchy process (AHP) is a multi-objective decision analysis method proposed by Professor Thomas L. Saaty at the University of Pittsburgh in the early 1970s. It is a common method for quantitative analysis of non-quantifiable factors in system engineering, and an effective method for the objective description of subjective judgments [2]. To apply the AHP, it is first necessary to determine the weight of each criterion indicator in the decision, and then make a weighted average of each indicator value in the alternative scheme based on the weight [3,4].
FAHP is a comprehensive and scientific evaluation method that builds upon the fuzzy comprehensive evaluation method and the AHP. It combines the advantages of both methods while addressing their shortcomings. Therefore, FAHP can accurately describe the weight of a criterion between any two factors with the advantages of solving the problems existing in the traditional AHP, improving the accuracy and rationality of qualitative and quantitative analysis, increasing the reliability of decision making, and making the evaluation results more accurate and reliable when used for evaluation [5].
Compared with the above methods, AHP is flexible and concise, suitable for multi-criteria decision-making problems. However, when there are numerous evaluation indicators, maintaining consistency in thinking becomes challenging, and the calculation process becomes complex. In contrast, FAHP enhances the ability to handle complex and fuzzy problems, making it ideal for issues with a large number of evaluation indicators or high fuzziness. The factor set that influences the evaluation results is determined based on the evaluation process and target requirements. Given the characteristics of the Business English Listening and Speaking Course, the FAHP method is selected to construct the evaluation model. In this model, the course evaluation factors are classified, hierarchically divided, and organized into the target layer, criterion layer, and indicator layer within the evaluation set, according to specific rules [6].
3.2 Determination of Evaluation Index Weight
Usually, [TeX:] $$\mathrm{U}=\left\{u_1, u_2, \ldots, u_n\right\}$$ represents each factor in the factor set. The subset of each factor is expressed as [TeX:] $$\mathrm{U}_{\mathrm{i}}=\left\{u_{i 1}, u_{i 2}, \ldots, u_{i k}\right\}(\mathrm{i}=1,2, \ldots, n),$$ and k is the number of factors of the subset. [TeX:] $$\mathrm{W}=\left[\mathrm{W}_1,\mathrm{W}_2, \ldots, \mathrm{~W}_n\right]$$ denotes the weight of each indicator and [TeX:] $$\mathrm{W}_i=\left[\mathrm{W}_{11}, \mathrm{~W}_{12}, \ldots, \mathrm{~W}_{1 \mathrm{i}}\right](i=1,2,3, \ldots, n)$$ indicates the weight of each indicator’s sub-indicators. The steps to calculate the weights of each criterion and the corresponding indicators of each criterion using FAHP are as follows [7].
1) Construction of a fuzzy complementary judgment matrix
The study adopts the expert scoring method, uses the 0.1–0.9 scale method in Table 1, analyzes the factors affecting the evaluation, compares the indicators with each other, and judges the relative importance of the index to their upper level indicators, to obtain the fuzzy complementary judgment matrix [TeX:] $$\mathrm{R}=\left(\mathrm{r}_{i j}\right)_{n \times n},(i, j=1,2, \ldots n), 0 \leq \mathrm{r}_{i j}\lt 1, \mathrm{r}_{ii}=0.5, \mathrm{r}_{i j}+\mathrm{r}_{j i}=1$$. When [TeX:] $$r_{ii}=0.5$$, it indicates that the factors are equally important compared; when [TeX:] $$0.5\lt \mathrm{r}_{i j} \leq 0.9,$$ it means that the factor [TeX:] $$\mathrm{r}_i$$ is more important than the factor [TeX:] $$\mathrm{r}_j.$$ Conversely, if [TeX:] $$0.1 \leq \mathrm{r}_{i j} \lt 0.5$$, it means that the factor [TeX:] $$\mathrm{r}_j$$ is more important than the factor [TeX:] $$\mathrm{r}_i$$.
Table 1.
| Scale | Definition | Explanation |
|---|---|---|
| 0.9 | Extremely more important | Compared with the two elements, the former is extremely more important. |
| 0.8 | Much more important | Compared with the two elements, the former is much more important. |
| 0.7 | Obviously more important | Compared with the two elements, the former is obviously more important. |
| 0.6 | Slightly more important | Compared with the two elements, the former is slightly more important. |
| 0.5 | Equally important | Both elements are equally important. |
| 0.4, 0.3, 0.2, 0.1 | Inverse ratio | If the element [TeX:] $$\mathrm{r}_i$$ is compared to [TeX:] $$\mathrm{r}_j$$ to get [TeX:] $$\mathrm{r}_{ij}$$, the inverse ratio of the two elements is [TeX:] $$\mathrm{r}_{ji}$$. |
2) Calculation of the index weight
If [TeX:] $$\mathrm{R}=\left(\mathrm{r}_{i j}\right)_{n \times n}$$ is the fuzzy complementary judgment matrix, using the formula to solve the relative weight of the index, [TeX:] $$\mathrm{W}=\left(\mathrm{W}_1, \mathrm{~W}_2, \ldots, \mathrm{~W}_i, \ldots, \mathrm{~W}_n\right)$$ is the weight vector of R. The formula is as follows:
In the formula, [TeX:] $$W_i$$ is the weight of factor [TeX:] $$\mathrm{r}_i$$.
3) Consistency test
The weight calculated through 1) needs to be checked for consistency in the comparison and judgment process to determine its rationality.
Based on the compatibility index I(A,B) of the judgment matrix and the definitions of feature matrix [TeX:] $$\mathrm{W}^*$$, the compatibility index of the judgment matrix and its characteristic matrix are calculated, and their expressions are as follows:
where, [TeX:] $$\mathrm{A}=\left(a_{i, j}\right)_{n \times n} \mathrm{~B}=\left(b_{i, j}\right)_{n \times n} \quad \mathrm{~W}^*=\left(\mathrm{W}_{i, j}\right)_{n \times n}.$$
(3)
[TeX:] $$\mathrm{W}_{i, j}=\mathrm{W}_i /\left(\mathrm{W}_i+\mathrm{W}_j\right) \forall i, j=1,2, \ldots, n|$$Among them, A and B are fuzzy complementary judgment matrices. If I(A,B) is less than a specific value α (generally α=0.1), the judgment matrix can be considered to be a satisfactory consistent matrix. The smaller α is, the higher the consistency requirement of the fuzzy judgment matrix is for decision makers.
3.3 Calculation of the Comprehensive Evaluation Results
The formative evaluation of students is set to m levels, and then the evaluation set is [TeX:] $$\mathrm{V}=\left\{\mathrm{v}_1, \mathrm{v}_2, \ldots, \mathrm{v}_m\right\} .$$ The membership degree of the evaluation index corresponding to each comment is the set on V, marked as [TeX:] $$\mathrm{R}_i$$:
The evaluation set of all indicators constitutes a fuzzy evaluation matrix R:
Finally, by multiplying the index weight vector W and the fuzzy comprehensive judgment matrix R to obtain [TeX:] $$\mathrm{B}=\mathrm{W} \bullet \mathrm{R},$$ the research determines the comprehensive evaluation matrix B, and gets the evaluation results according to the maximum membership principle.
4. Construction of Formative Evaluation System Model
4.1 Determination of Evaluation Indicators
In the Business English Listening and Speaking Course, formative evaluation involves many factors, some of which can be quantified, while others cannot. For example, the comprehensive evaluation of students’ learning performance, and other aspects that are difficult to be quantified can only be made by qualitative analysis, and the evaluation of various factors (or activities) is generally fuzzy.
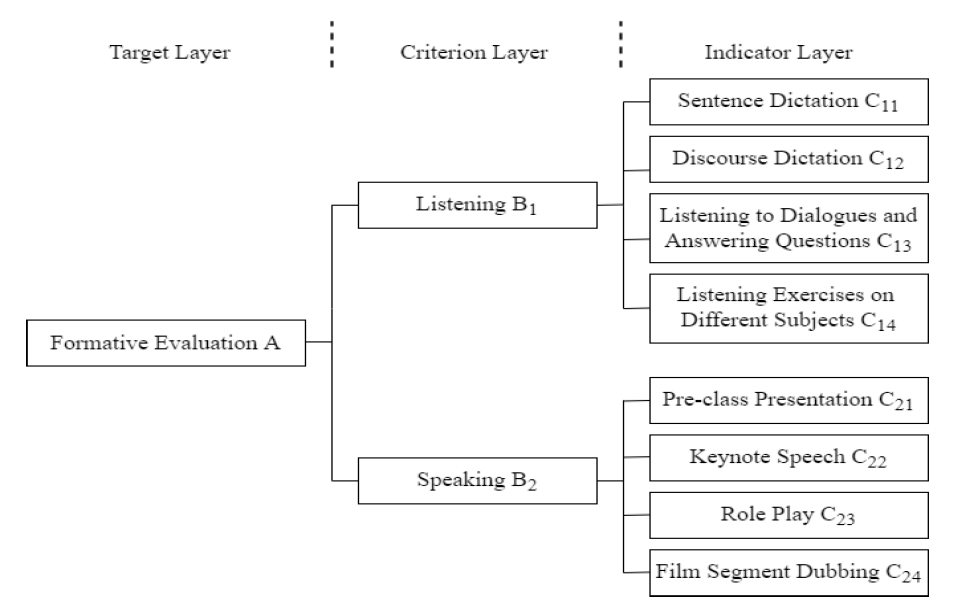
Eight activities are designed for formative evaluation based on the two practical skills of business listening and speaking aligned with the course objectives. The listening activities include sentence dictation, discourse dictation, listening to dialogues and answering questions, and listening exercises on different subjects. The oral performance tasks include pre-class presentations, keynote speeches, role play, and film segment dubbing. Consequently, these eight activities are utilized to construct an evaluation model for the course’s formative evaluation.
The first layer of the evaluation model is the target layer A (formative evaluation). The second layer is the criterion layer B (including language skills of listening [TeX:] $$\mathrm{B}_1$$ and speaking [TeX:] $$\mathrm{B}_2$$). The third layer is the indicator layer C (consisting of eight indicators: sentence dictation [TeX:] $$\mathrm{C}_{11},$$ discourse dictation [TeX:] $$\mathrm{C}_{12},$$ listening to dialogues and answering questions [TeX:] $$\mathrm{C}_{13},$$ listening exercises on different subjects [TeX:] $$\mathrm{C}_{14},$$ pre-class presentation [TeX:] $$\mathrm{C}_{21},$$ keynote speech [TeX:] $$\mathrm{C}_{22},$$ role play [TeX:] $$\mathrm{C}_{23},$$ and film segment dubbing [TeX:] $$\mathrm{C}_{24},$$), as shown in Fig. 1.
The evaluation index set of the FAHP model is as follows:
4.2 Determination of the Weight Indicator Vector
The Delphi survey method was used for survey statistics, and 20 peer experts and frontline teachers were invited as the survey respondents. In the form of an online questionnaire, the questionnaire was sent to the respondents according to the rules and steps of the evaluation requirements. After several rounds of consultation and statistical modification, the consensus was reached to ensure the objectivity and authenticity of the survey results. Statistics were made on the questionnaire, the weight of each index was determined, and the fuzzy judgment matrix was established. The results are shown in Table 2.
Table 2.
| A | [TeX:] $$\mathrm{B}_1$$ | [TeX:] $$\mathrm{B}_2$$ |
|---|---|---|
| [TeX:] $$\mathrm{B}_1$$ | 0.5 | 0.605 |
| [TeX:] $$\mathrm{B}_2$$ | 0.395 | 0.5 |
According to the formula (1), the weight of each index of matrix A-B is W= (0.5525, 0.4475), and based on (2) and (3), the compatibility indicator value of the judgment matrix and its feature matrix is 0.02625 < 0.1, which conforms to the consistency verification.
Similarly, the fuzzy judgment matrix (B1-C and B2-C) of criterion and scheme layers can be constructed, as shown in Tables 3 and 4.
Table 3.
| [TeX:] $$\mathrm{B}_1$$ | [TeX:] $$\mathrm{C}_{11}$$ | [TeX:] $$\mathrm{C}_{12}$$ | [TeX:] $$\mathrm{C}_{13}$$ | [TeX:] $$\mathrm{C}_{14}$$ |
|---|---|---|---|---|
| [TeX:] $$\mathrm{C}_{11}$$ | 0.5 | 0.34 | 0.37 | 0.3 |
| [TeX:] $$\mathrm{C}_{12}$$ | 0.66 | 0.5 | 0.46 | 0.39 |
| [TeX:] $$\mathrm{C}_{13}$$ | 0.63 | 0.54 | 0.5 | 0.41 |
| [TeX:] $$\mathrm{C}_{14}$$ | 0.7 | 0.61 | 0.59 | 0.5 |
Table 4.
| [TeX:] $$\mathrm{B}_1$$ | [TeX:] $$\mathrm{C}_{11}$$ | [TeX:] $$\mathrm{C}_{12}$$ | [TeX:] $$\mathrm{C}_{13}$$ | [TeX:] $$\mathrm{C}_{14}$$ |
|---|---|---|---|---|
| [TeX:] $$\mathrm{C}_{11}$$ | 0.5 | 0.41 | 0.45 | 0.46 |
| [TeX:] $$\mathrm{C}_{12}$$ | 0.59 | 0.5 | 0.48 | 0.51 |
| [TeX:] $$\mathrm{C}_{13}$$ | 0.55 | 0.52 | 0.5 | 0.48 |
| [TeX:] $$\mathrm{C}_{14}$$ | 0.54 | 0.49 | 0.52 | 0.5 |
According to the formula (1), the weight of the indicator [TeX:] $$\mathrm{B}_1$$ is as follows: [TeX:] $$\mathrm{W}_1=(0.209,0.251,0.257,0.283), \text { and } \mathrm{I}\left(\mathrm{~B}_1, \mathrm{~W}_1\right)=0.0639\lt 0.1$$ can be obtained from the formulas (2) and (3). In the same way, [TeX:] $$\mathrm{W}_2=(0.235,0.257,0.254,0.254), \text { and } \mathrm{I}\left(\mathrm{~B}_2, \mathrm{~W}_2\right)=0.0211\lt 0.1.$$
Therefore, the fuzzy judgment matrices B1-C and B2-C both pass consistency verification.
4.3 Calculation of the Formative Evaluation Results
The evaluation process includes both qualitative and quantitative evaluation methods. There are two categories of evaluation criteria, [TeX:] $$\mathrm{B}_1 \text { and } \mathrm{B}_2 .$$ [TeX:] $$\mathrm{B}_1$$ comprises four secondary indicators: sentence dictation, discourse dictation, listening to dialogue and answering questions, and listening exercises on different subjects, which are suitable for quantitative evaluation method and can be directly quantified and graded based on test scores. B2 includes four indicators: pre-class presentation, keynote speech, role-playing, and film segment dubbing, which are suitable for qualitative evaluation methods. The evaluation information is first collected and presented in a non-numerical form. The study employs Likert scale method to define the evaluation into five levels: excellent, good, medium, qualified, and unqualified. Subsequently, corresponding evaluation indicators are assigned based on the learning behavior of the evaluated object.
5. System Instance Implementation
5.1 System Functions and Environment Deployment
The system includes two roles: users and evaluators. Users log in to query evaluation results, while evaluators log in to complete evaluations. The system is deployed using a B/S architecture mode, and its database is designed based on Oracle. In terms of hardware configuration, the system consists of two Web servers and one database server.
5.2 Implementation Process of the Evaluation System
A review panel comprising the course instructor and nine students evaluates the performance of all students in the class. To ensure the fairness, participation, and effectiveness of the evaluation process, a detailed evaluation procedure is designed. Students are initially screened based on their academic performance, interests, and sense of responsibility to establish a pool of potential reviewers. Reviewers are then selected through random selection process. When assessment scoring, the reviewers strictly follow the course evaluation criteria, grading methods, and precautions outlined by the system, scoring item by item. The system calculates and aggregates the evaluation data for each student to produce comprehensive and objective evaluation results. This evaluation approach provides a just and impartial evaluation environment for students’ learning journey. Below is the calculation process for the evaluation data of a certain student within the system.
1) Calculations of the evaluation results of the secondary indicators
Secondary indicators include B1 and B2. The membership degree of B1 indicator can be directly quantified and graded, and the judgment matrix R1 is obtained according to the score statistics
Utilizing the weight coefficient of index layer and criterion layer, the comprehensive evaluation is carried out:
where [TeX:] $$^\circ$$ is a fuzzy synthesis operator.
According to the operation rules of weight set [TeX:] $$\mathrm{W}_i$$ and single factor fuzzy evaluation matrix [TeX:] $$\mathrm{R}_i,$$ the evaluation fuzzy subset [TeX:] $$\mathrm{B}_i,$$ is obtained. But considering the multifactorial influence on student evaluation results, the comprehensive weighted average type [TeX:] $$\mathrm{M}(\bullet, \oplus)$$ is used for synthesis operation.
The evaluation matrix for [TeX:] $$\mathrm{B}_2$$ evaluation results is [TeX:] $$\mathrm{R}_2$$:
Same as [TeX:] $$\mathrm{B}_1, \mathrm{~B}_2=\mathrm{W}_2{ }^{\circ} \mathrm{R}_2=\left(\begin{array}{lllll} 0.247 & 0.428 & 0.226 & 0.074 & 0\end{array}\right),$$ normalized to (0.253, 0.439, 0.232, 0.076, 0) [8].
2) Multilevel fuzzy comprehensive evaluation model
Using the weight coefficients of the target layer and the criterion layer, a fuzzy comprehensive evaluation of the student is obtained.
By utilizing the weight coefficients of the target layer and the criterion layer, fuzzy comprehensive evaluation can be conducted on students.
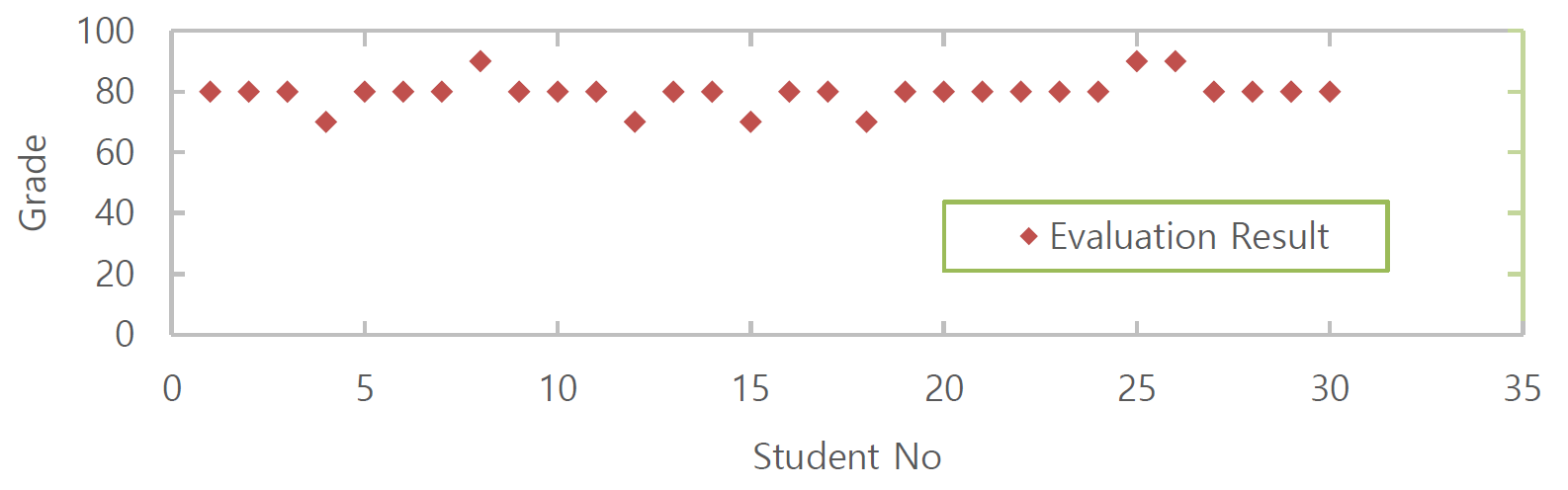
The evaluation result of the student can be obtained through system calculation: the evaluation result is excellent with a membership degree of 37.6%, good with a membership degree of 33.5%, intermediate with a membership degree of 26%, and poor with a membership degree of 3.4%. According to the principle of maximum membership degree, the student’s evaluation level is deemed “excellent.” The system processed the evaluation data of 30 students in the class and obtained the evaluation results for each student. The results were categorized into grades: excellent (90), good (80), medium (70), qualified (60), and unqualified (below 60). The distribution of formative evaluation data for all students in the class is shown in Fig. 2.
The evaluation results obtained through the FAHP method, as depicted in Figure 2, demonstrate significant advantages over the conventional results in the form of a curve generated by simply averaging teachers’ subjective scores, where students’ differences are not clearly delineated. This method employs algorithms to transform fuzzy information that is difficult to quantify, as well as information about the process of learning, into quantifiable numerical values that serve as evaluation indicators. This approach makes the evaluation process more aligned with students’ actual performance and effectively mitigates the influence of subjective judgments. Moreover, it can accurately and objectively illustrate the gap between students’ learning achievements and the excellent level.
Additionally, the evaluation data are not solely used for categorizing students’ abilities into distinct levels; instead, they are specifically employed to assess teachers’ teaching quality. The data collection and computation process adopts a closed-loop management system, which is designed to enhance teaching quality. It is utilized to provide personalized instructional guidance tailored to each student’s unique needs, thereby enabling teaching to be adapted to their specific requirements (i.e., “teaching students according to their aptitude”). This approach effectively safeguards against the leakage of sensitive evaluation data.
6. Conclusion
This paper applies the FAHP method to conduct a detailed hierarchical analysis of the students’ learning process, aiming to uncover various factors that affect learning effectiveness. Utilizing the expert analysis method, the research constructs a comprehensive evaluation system model, which transforms the formative assessment data into quantitative results through scientific methodologies, thereby ensuring the objectivity and accuracy of the evaluation.
In the Business English Listening and Speaking Course, the application of formative evaluation is not merely a test of students’ achievements, but also an embodiment of their independent learning process. With the assistance of detailed analysis of formative evaluation, teachers gain precise insights into the learning status of each student, and then reflect on their teaching and make targeted adjustments. The fuzzy comprehensive evaluation model equips students with a self-evaluation standard, helping them better understand their learning progress and breaking the limitations of traditional exams that solely focus on results and ignore processes. This evaluation approach not only enhances the learning experience of students, but also fosters the reform of teaching modes. The construction and implementation of the formative evaluation system model advance the digital application of the teaching process and broadens the horizons for the integration of information technology and education. This system model not only aids teachers in gaining a more precise understanding of students’ learning status, but also provides more timely and effective feedback for students, thereby optimizing the teaching process and elevating the quality of education.
Funding
This work was supported by Construction of a Comprehensive Business English Smart Course Based on the Xuexitong Platform, the Education and Teaching Reform Research Project from Higher Education Research Institute of Hebei North University (No. JG202529); Sports Science and Technology Research Project in Hebei Province of China (No. 2023QT08); and Research on the Application of Blockchain Technology in College Student Status Management (No. 2221024B).
Biography
Huifang Shan
https://orcid.org/0009-0007-3170-9759She received B.S. degree in English language and literature from Hebei Normal University in 2001 and M.S. degree in English linguistics from Tianjin University of Technology in 2007, respectively. She is currently a teacher of business English in the School of Foreign Studies, Hebei North University, Zhangjiakou. Her current research interests include the application of information technology in the English classes.
Biography
Junrui Han
https://orcid.org/0000-0002-0803-1130He received B.S. degree in the Department of computer science and technology from Beijing Institute of Information Engineering in 2002, and M.S. degree in computer application from Hebei University of Engineering in 2011. He is currently an engineer in the Office of Educational Administration, Hebei North University, Zhangjiakou, China. His research interests include information processing and privacy protection.
Biography
Zhanfang Li
https://orcid.org/0000-0002-0910-5189She received M.S. degree and PhD. degree in English linguistics from Beijing Normal University in 2003 and in 2007, respectively. She is currently a teacher in the School of Foreign Studies, North China Electric Power University, Beijing. Her current research interests include the application of information technology in the English classes.
References
- 1 W. Wang, "Construction of a precision poverty alleviation satisfaction evaluation index system based on AHP theory," Statistics and Decision-Making, vol. 36, no, 15, pp. 60-64, 2020. https://doi.org/10.13546/j.cnki. tjyjc.2020.15.012doi:[[[10.13546/j.cnki.tjyjc.2020.15.012]]]
- 2 Z. Li, Q. Dang, H. Li, T. Liu, and Y . Zhang, "Evaluation and optimal selection of invisible orthodontic schemes based on analytic hierarchy process," Journal of Graphics, vol. 42, no. 5, pp. 856-865, 2021.custom:[[[-]]]
- 3 Y . Bing, W. Wang, S. Sun, X. Liu, Q. Nie, and J. Liu, "Network reliability analysis of power monitoring system based on improved fuzzy comprehensive evaluation method," Computer Science, vol. 50, no. 6A, pp. 774-780, 2023. https://doi.org/10.11896/jsjkx.220400293doi:[[[10.11896/jsjkx.20293]]]
- 4 C. Li, S. Shen, and M. Xu, "Construction and empirical research on the evaluation index system of urban "three lives" environmental quality," Statistics and Decision-Making, vol. 36, no. 22, pp. 61-65, 2022. https://doi.org/10.13546/j.cnki.tjyjc.2020.22.014doi:[[[10.13546/j.cnki.tjyjc.2020.22.014]]]
- 5 L. Tang, C. Ni, and H. Li, "Supply and demand matching method of coating design cloud service based on demand satisfaction," Machine Design & Research, vol. 39 no. 4, pp. 178-184, 2023. https://doi.org/10. 13952/j.cnki.jofmdr.2023.0159doi:[[[10.13952/j.cnki.jofmdr.2023.0159]]]
- 6 D. Sharma, S. Sridhar, and D. Claudio, "Comparison of AHP-TOPSIS and AHP-AHP methods in multicriteria decision-making problems," International Journal of Industrial and Systems Engineering, vol. 34, no. 2, pp. 203-223, 2020. https://doi.org/10.1504/IJISE.2020.105291doi:[[[10.1504/IJISE.2020.105291]]]
- 7 R. Lai, W. Lin, and Y . Wu, "Redesign priority identification of product family modules for green performance optimization," China Mechanical Engineering, vol. 30, no. 11, pp. 1329-1335, 2019. https://doi.org/10.3969/ j.issn.1004-132X.2019.11.010doi:[[[10.3969/j.issn.1004-132X.2019.11.010]]]
- 8 H. Yao, J. Liu, E. Tong, and W. Niu, "CTCS network security risk assessment method based on α-cut triangular fuzzy number and attack tree," Journal of Computer Applications, vol. 44, no. 4, pp. 1018-1026, 2024.custom:[[[-]]]