Xiaoling Guo , Xinghua Sun , Ling Li , Renjie Wu and Meng Liu
Centralized Clustering Routing Based on Improved Sine Cosine Algorithm and Energy Balance in WSNs
Abstract: Centralized hierarchical routing protocols are often used to solve the problems of uneven energy consumption and short network life in wireless sensor networks (WSNs). Clustering and cluster head election have become the focuses of WSNs. In this paper, an energy balanced clustering routing algorithm optimized by sine cosine algorithm (SCA) is proposed. Firstly, optimal cluster head number per round is determined according to surviving node, and the candidate cluster head set is formed by selecting high-energy node. Secondly, a random population with a certain scale is constructed to represent a group of cluster head selection scheme, and fitness function is designed according to inter-cluster distance. Thirdly, the SCA algorithm is improved by using monotone decreasing convex function, and then a certain number of iterations are carried out to select a group of individuals with the minimum fitness function value. From simulation experiments, the process from the first death node to 80% only needs about 30 rounds. This improved algorithm balances the energy consumption among nodes and avoids premature death of some nodes. And it greatly improves the energy utilization and extends the effective life of the whole network.
Keywords: Centralized Clustering Routing Algorithm , Energy Balance , LEACH , Sine Cosine Algorithm , WSNs
1. Introduction
Wireless sensor networks (WSNs) is a self-organizing dynamic network and consists of many micro intelligent sensor nodes distributed in different geographical locations. These sensor nodes intercommunicate by multi-hop and wireless communication mode. They can collaboratively perceive, calculate, and transmit the collected data and report to the observer. Due to some limitations, such as cost and shape, sensor nodes are battery powered and carry limited power energy. Therefore, the primary goal of WSNs is to use power energy as efficiently as possible and prolong the lifetime of sensor nodes.
Low energy adaptive clustering hierarchy (LEACH) proposed by Heinzelman et al. [1], which is the first clustering routing algorithm. LEACH periodically and randomly selects cluster heads, which are responsible for organizing communications of member nodes within the cluster. Cluster head fuses the information within the cluster and relays them to the base station. LEACH algorithm can ensure that each node can be the cluster head only once in every cycle. In this way, energy consumption is assigned to every sensor node. This approach helps to prolong network life cycle.
But LEACH is a distributed cluster routing protocol. LEACH cannot guarantee the optimal number and scale of clusters generated in each round and it is also not applicable if base station is far away from the monitoring region. Because long-distance transmission will consume more energy. In addition, LEACH does not consider residual energy when selecting cluster heads. Once low-energy nodes are selected as cluster heads, their energy is quickly consumed out and nodes will die. Therefore, clustering and cluster head election have become the focuses of WSNs.
2. Literature Overview and Related Research
About how to cluster and elect cluster heads, a lot of research have been done. One kind of research starts from cluster head election conditions, such as calculating residual energy, considering distance, ensuring appropriate size of cluster, etc.
In [2], selection function of cluster head is optimized. The effective radius of base station receiving messages, the inter-cluster distance, and distribution of the nodes are introduced. And the conditions for whether the node can be repeatedly elected as the head node are added to the head node selection function. However, the algorithm needs to be further improved in balancing the energy consumption among nodes. In [3], communication cost is designed. Node with small communication cost and more residual energy is selected as relay node for communication. However, inter-cluster multi-hop communication mechanism is used to lead to increase the complexity. Li et al. [4] points out that cluster head nodes usually consume more energy. Cluster head number cannot be too many or too few. It is necessary to set appropriate number of cluster head. In this paper, average energy consumption of the network is the lowest when nodes obey the two-dimensional Poisson Distribution. It uses the method in LEACH algorithm to improve network lifetime. The relevant conclusions can provide theoretical support for clustering. In [5], the states of adjacent cluster heads and adjacent nodes are considered, and the nodes are processed by levels. In the cluster head selection stage, the cluster heads are re-optimized according to cluster range and cluster position, so as to avoid the problems of unreasonable cluster range. In the data transmission stage, relay nodes are used to balance node energy consumption. The selection of relay nodes is comprehensively worked out by residual energy, distance among nodes and adjacent nodes. This algorithm is a distributed routing algorithm. It is an optimization based on local neighboring nodes. In the study of Kim et al. [6], the necessary conditions for improving energy efficiency are analyzed using clustering and location-based routing technology. A clustering formula is proposed based on energy and distance, establishes the path from each channel to base station and improves the way of collecting data.
Another kind research is centralized cluster head election. Base station uses population optimization algorithm to select the appropriate cluster head scheme.
For example, in [7], a combination of centralized and distributed methods is mentioned to cluster and elect cluster head. K-Medoids clustering method optimized by genetic algorithm is used. Cluster heads are elected by considering geographical location, residual energy and the number of rounds that have served as cluster head. The best communication object according to distance is selected, and polling mechanism is introduced into the intra-cluster communication. In [8], butterfly optimization algorithm (BOA) is executed according to the distance to adjacent nodes and base station, residual energy, node degree and node centrality. Ant colony optimization (ACO) is applied to identify the route from cluster heads to base station, and select optimal route according to node degree, distance, and residual energy. Two optimization algorithms are used in this paper, and the running time of the program may be long. In [9], the optimized black hole algorithm is in use. It is optimized by free buffer, residual energy, and distance. ACO is used to find the path. Black hole algorithm and ACO algorithm are combined to improve network lifetime. Ajmi et al. [10] proposed MWCSGA (multi weight chicken swarm based genetic algorithm). It includes chicken swarm optimization, genetic algorithm, CCSO-GA cluster head selection, multi weight clustering model, inter-cluster, and intra-cluster communication. The algorithm is relatively complex, system running time is relatively long, and the burden of base stations and sensor nodes are also heavy. In [11], the algorithm is called CRISCA (clustering routing protocol based on improved sine cosine algorithm). It introduces inertia weight factor and improves sine cosine algorithm (SCA). It combines the distance among nodes, among nodes and base stations and the residual energy of nodes to build a fitness function. But the energy efficiency of this algorithm is not very ideal.
3. Improvements to SCA
It is not difficult to realize that the centralized clustering algorithm has a better energy utilization and a longer network life than the distributed clustering algorithm. In the centralized clustering algorithm, in order to try to reduce the cost of each round of communication, the population optimization algorithm is often used, or even more than two population optimization algorithms are used.
In 2016, Mirjalili [12] proposes SCA algorithm that uses sine mathematical or cosine mathematical model to carry out location update by creating multiple random candidate solutions. SCA algorithm can be used for clustering routing algorithm. This can reduce the data communication consumption in each round and improve energy utilization.
Assuming that population size is Q, and the dimension of each individual is K, then the spatial position of individual i in the j dimension is expressed as [TeX:] $$X_{i j}$$, iterate calculation process is executed according to formula (1):
(1)
[TeX:] $$X_{i j}(t+1)= \begin{cases}X_{i j}(t)+r_1 \sin r_2\left|r_3 X_j^*(t)-X_{i j}(t)\right|, r_4 \lt 0.5 \\ X_{i j}(t)+r_1 \cos r_2\left|r_3 X_j^*(t)-X_{i j}(t)\right|, r_4 \geq 0.5\end{cases}$$In formula (1), [TeX:] $$i \in\{1,2, \ldots, Q\}, j \in\{1,2, \ldots, K\}, X_j^*(t)$$ is the current optimal individual at the t iteration, [TeX:] $$r_1, r_2, r_3 \text {, and } r_4$$ are random parameters, [TeX:] $$r_2 \in[0,2 \pi], r_3 \in[0,2] \text { and } r_4 \in[0,1]$$. [TeX:] $$r_1$$ is related to t, seen from formula (2):
In formula (2), t is a constant, usually be 2. means current iteration number, and T means maximum iteration number.
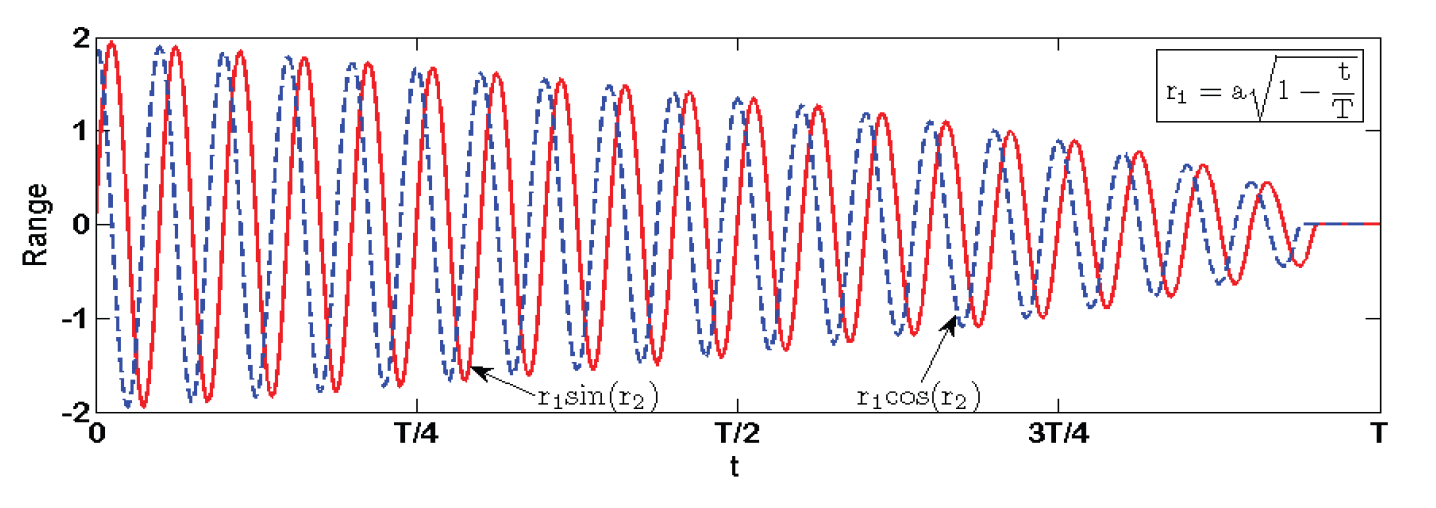
From the formula (1) and formula (2), it can be seen that only when [TeX:] $$r_1 \gt 1$$, sine function value [TeX:] $$r_1 \sin \left(r_2\right)$$ or cosine function value [TeX:] $$r_1 \cos \left(r_2\right)$$ can be greater than 1 or less than -1, SCA algorithm explores solution in a large space. When [TeX:] $$r_1 \leq 1$$, sin function value [TeX:] $$r_1 \sin \left(r_2\right)$$ or cosine function value [TeX:] $$r_1 \cos \left(r_2\right)$$ must be between -1 and 1 [13], SCA algorithm explores the solution in a relatively small local region. According to the design principle of SCA algorithm, the algorithm first carries out global exploration, then local development. Therefore, [TeX:] $$r_1$$ is an important parameter for controlling transformation from global exploration to local development [14], as shown in Fig. 1.
In standard SCA function above, [TeX:] $$r_1$$ is a linear decreasing, and its function value gradually decreases linearly to 0 with the increase of iteration times t as shown in Fig. 2.
Fig. 2.
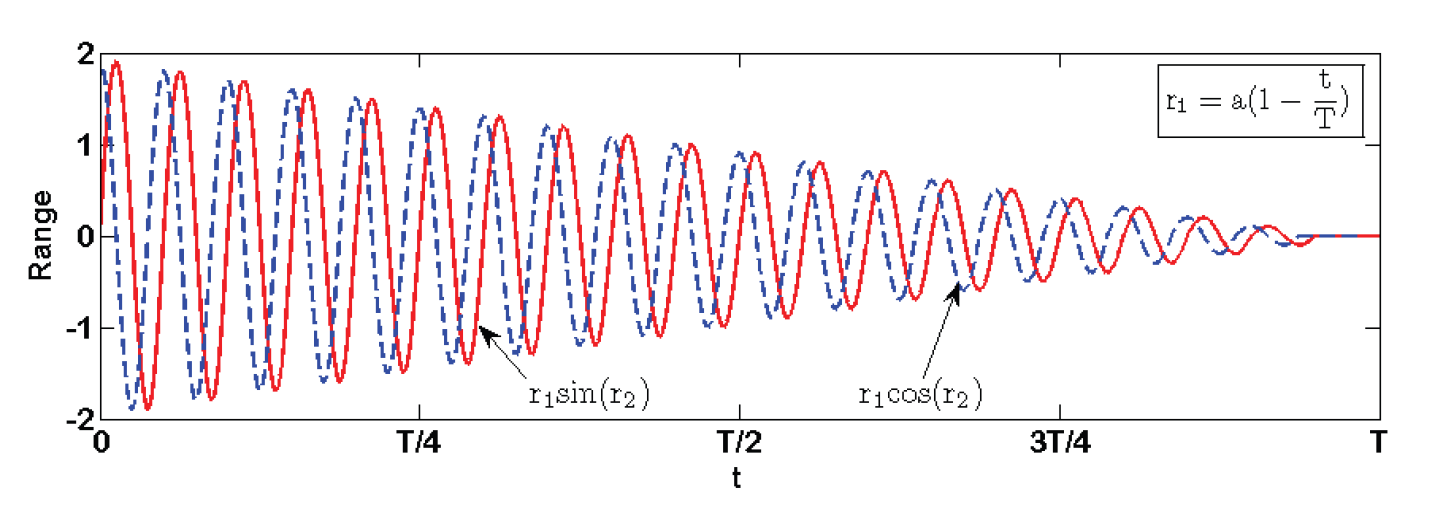
From Fig. 2, it can be seen that SCA algorithm may fall into local extremum [15]. Moreover, when solution space is large, the SCA algorithm shows the problem of low optimization accuracy. It is difficult to find the optimized cluster head scheme. Therefore, in order to increase its space exploration ability as much as possible, it is necessary to provide enough random solutions. So [TeX:] $$r_1$$ is designed as monotonically decreasing convex function in formula (3). It makes the variation range of sine cosine function value as Fig. 3. By comparing Fig. 3 with Fig. 2, it is found that improved SCA can strengthen local development and expand the search scope. Formula (3) can well avoid premature of individual optimal solution and help to find a relatively optimal cluster head scheme.
SCA can be used for cluster routing algorithm. Q represents a group of random cluster head selection schemes, and [TeX:] $$X_{i j}$$ represents an optimal cluster head scheme in the current group of schemes, that is, a cluster head scheme with the minimum fitness function value [16]. Using the formula (1) and formula (3) to perform a certain number of iterations, we can select an optimal scheme with minimum communication cost in a large search space as final clustering.
4. Proposed Algorithm and Implementation
4.1 Energy Consumption Model
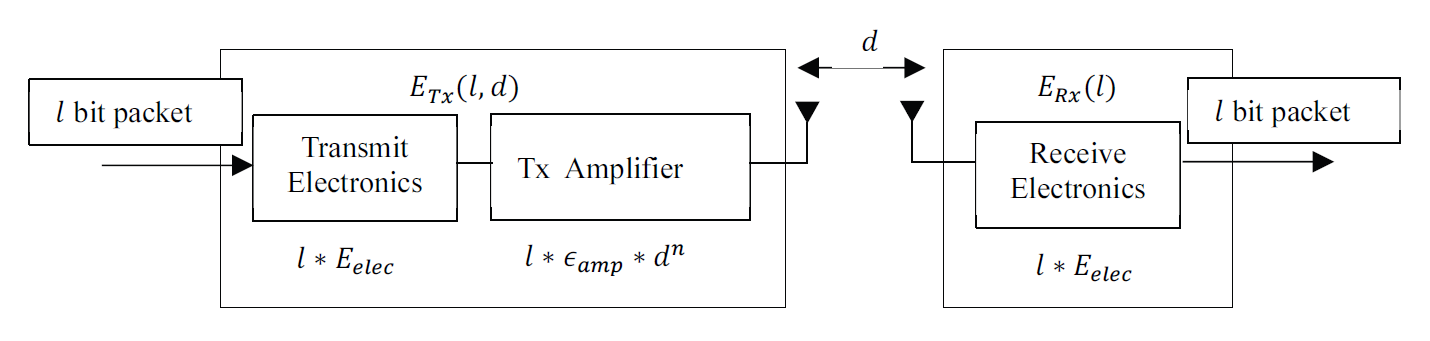
The energy consumption model [17] is shown in Fig. 4.
In Fig. 4, l represents bit data and d distance. [TeX:] $$E_{\text {elec }}$$ is the energy consumption per-unit data. [TeX:] $$\epsilon_{f s}$$ and [TeX:] $$\epsilon_{m p}$$ are coefficient of power amplifier, and they respectively correspond to free space model and multipath fading model. They are as follows:
Sending data is calculated according to the formula (4):
(4)
[TeX:] $$\begin{gathered} E_{T x}(l, d)=E_{T x-e l e c}(l)+E_{T x-a m p}(l, d) \\ \quad= \begin{cases}l E_{\text {elec }}+l \epsilon_{f s} d^2, d \lt d_o \\ l E_{\text {elec }}+l \epsilon_{m p} d^4, d \geq d_0\end{cases} \end{gathered}$$In it, [TeX:] $$d_o=\sqrt{\frac{\epsilon_{f s}}{\epsilon_{m p}}}=87$$.
Receiving data is calculated according to the formula (5):
During data fusion, n means total node numbers in a cluster. l bit data is transferred to cluster head, and data fusion is calculated according to the formula (6):
In it, [TeX:] $$E_{D A}=5 n J / b i t / s i g n a l .$$
4.2 Calculation of the Numbers of Cluster Head per Round
N represents total sensor nodes in monitoring area. These sensor nodes are arranged in the scope of M×M. k represents the numbers of cluster head in each round. [TeX:] $$E_{C H}$$ is used to represent cluster head’s energy consumption. It is calculated with formula (7). [TeX:] $$E_{C H}$$ includes receiving local transmission, local fusion and relaying to the base station [18].
(7)
[TeX:] $$E_{C H}=l E_{e l e c}\left(\frac{N}{k}-1\right)+l E_{D A} \frac{N}{k}+l E_{e l e c}+l \epsilon_{m p} d_{t o B S}^4.$$[TeX:] $$E_{n o n-C H}$$ is used to represent cluster member’s energy consumption. In each round, cluster member only communicates with cluster head. [TeX:] $$E_{n o n-C H}$$ is shown in formula (8).
[TeX:] $$k_{o p t}$$ represents the optimal number of cluster head. [TeX:] $$k_{o p t}$$ is obtained with the formula (9) according to the literature [18].
(9)
[TeX:] $$k_{o p t}=\frac{\sqrt{N}}{\sqrt{2 \pi}} \sqrt{\frac{\epsilon_{f s}}{\epsilon_{m p}}} \frac{M}{d_{t o B S}^2} .$$p is used to represent cluster head election probability. p is calculated according to [TeX:] $$p=\frac{k_{\text {opt }}}{N}$$ in [19], then it can be converted to formula (10).
N represents surviving sensor nodes in current network in formula (10). When death nodes appear, k should change proportionally, and be calculated according to the formula (11). N-dead indicates surviving nodes.
4.3 Construction of Fitness Function
There are two kinds of distances: intra-cluster and inter-cluster distance. The weights of two distances in the fitness function are different for different network sizes, which are related to the scope of network (M×M), nodes total number (N), cluster head number (k) and location of base station. For the improved algorithm in this paper, the simulation is carried out in 200 m × 200 m with 200 nodes, and base station is outside the region. This is a larger monitoring network than LEACH, and inter-cluster distance has become the primary consideration. After repeated experiments, it is found that intra-cluster distance has a very small impact on improving the network life, prolonging about 10 rounds. If intra-cluster distance is considered when designing fitness function, it will increase the computational complexity. Based on this, only inter-cluster distance is considered when designing fitness function of SCA. So it is designed as the formula (12). In formula (13), [TeX:] $$d_{t o B S}$$ represents the inter-cluster distance.
(13)
[TeX:] $$D(i)=\left\{\begin{array}{ll} d_{t o B S}^2(i) d_{t o B S}(i) \lt d_o \\ d_{t o B S}^4(i) d_{t o B S}(i) \geq d_0 \end{array} .\right.$$4.4 Cluster Division Phase
4.4.1 Building candidate cluster head set
Average energy value (AVE) of current surviving nodes are calculated in base station at the beginning of each round. The improved algorithm selects nodes with energy greater than or equal to AVE to form candidate cluster-head set (C). In formula (14), S(i).E represents current energy, [TeX:] $$S_{\text {alive }}(i).$$ E stands for surviving node’s energy.
(14)
[TeX:] $$C=\left\{i, i \in N, 1 \leq i \leq N, S(i) . E \geq A V E\left(S_{\text {alive }}(i) . E\right)\right\}$$The elements in the set C should be greater than k. If it is less than k, the base station will gradually cut down the selection condition with formula (15) until the elements in the set C is greater than or equal to k. In the formula (15), scaDnum starts from 0 and adds 1 each time, that is, the selection condition would become greater than or equal to 9/10 of the average energy. If the elements in the set C is still less than k, the selection condition would be cut down to (9–1)/10, and so on.
(15)
[TeX:] $$S(i).E \geq A V E\left(S_{\text {alive }}(i). E\right) *(9-\text { scaDnum }) / 10 .$$4.4.2 Electing optimal cluster head
The optimal cluster head number is calculated with surviving nodes and cluster head probability. Then, the base station determines candidate cluster head set according to residual energy and then generates the initial random population. Inter-cluster distance is used to construct fitness function. The improved SCA algorithm is used to select the optimal clustering scheme after a certain number of iterations.
(1) From set C, k nodes are randomly selected each time to represent one kind of cluster head selection scheme. Select Q times to form population. The fitness function value of each individual is compared in the population, then minimum fitness function selected as the current optimal individual [TeX:] $$X_j^*(t)$$.
(2) Update each individual with formula (1) and formula (3). If the updated value exceeds the limit, replace it with the corresponding cluster head of the current optimal individual; if the updated node is not in set C, select the nearest node in set C as updated cluster head; if it is duplicated, a non-duplicated node is randomly selected from set C to replace the duplicate cluster head.
(3) After each iteration update, the fitness function value is recalculated, new optimal individual selected, and it would be compared with the previous one. The improved algorithm preserves a group of individuals with the minimum fitness function to participate in the next iteration.
(4) After all iterations, the individual with the minimum fitness function value retained would become the cluster heads.
The steps of electing optimal cluster head are as followings:
4.5 Cluster Formation Phase
After selecting cluster head, the base station broadcasts cluster head ID. If broadcast ID matches the node own ID, it will be cluster head; if not, the node will establish contact with the nearest cluster head. It will become its cluster member node, then wait for the arrival of the corresponding TDMA time slot to transmit data. Member nodes send data on the basis of allocated time slot. Other nodes will sleep automatically. Cluster head nodes receive data, carry on fusion and relay them to base station. So far, the cluster division is completed. After the algorithm is executed for a period of time, the base station will conduct next round of election and clustering, and the network will start a new data transmission stage.
5. Simulation and Analysis
5.1 Parameter Settings
In the paper, MATLAB R2010b software is used for programming and simulation. 200 nodes are randomly arranged in 200 m×200 m. After being deployed, the position of the nodes will not change any longer, and the initial energy is 0.5 J. The base station is at x = 100 m, y = 250 m. It is assumed that base station energy is infinite. Cluster head selecting probability is p=0.05, the packet transmitted by nodes in each round is 4000 bits, the maximum iterations is 20, and the number of populations is 15, as shown in Table 1.
Table 1.
| Parameter | Value |
|---|---|
| Region | 200 m×200 m |
| Node number (N) | 200 |
| Node initial energy | 0.5 J |
| Base station coordinates | (100 m, 250 m) |
| Cluster head selection probability (p) | 0.05 |
| l packet size | 4000 bits |
| Maximum iterations | 20 |
| Population | 15 |
| Maximum rounds | 1,500 |
5.2 Results and Analysis
To analyze the improved algorithm, we compare it with LEACH and CRISCA from three aspects: network life cycle, energy balance, and throughput.
5.2.1 Network life cycle
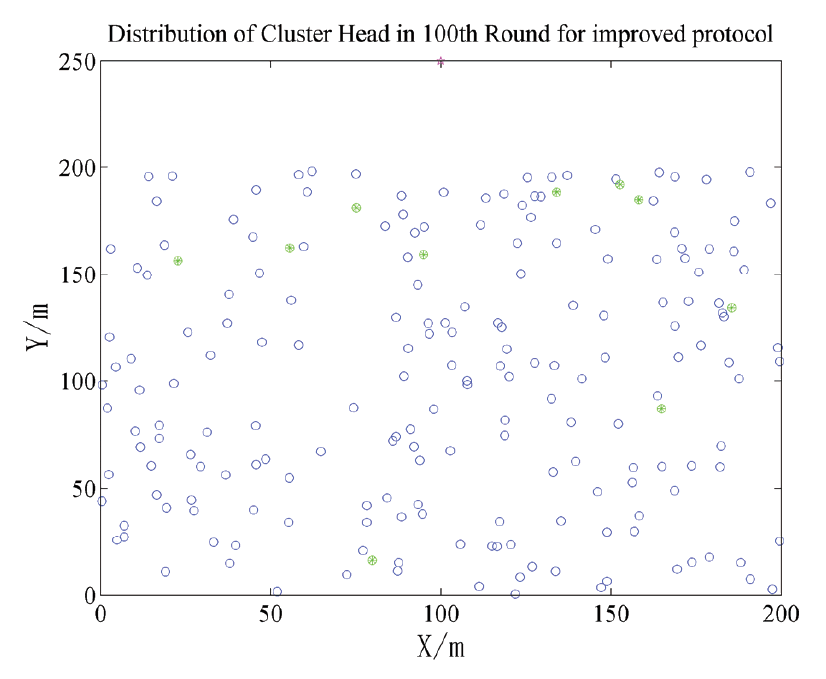
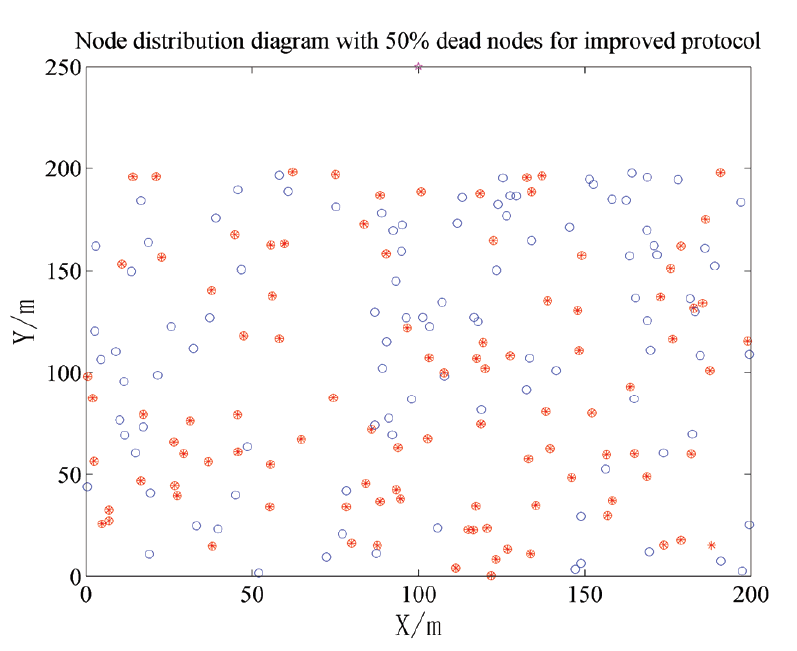
The green solid point is the cluster head node, the blue hollow circle is the member node, and the five-pointed star at the top is the base station. In Fig. 5, improved algorithm elects cluster heads according to the probability of 0.05. Before appearing dead node, the numbers of cluster head are fixed to be 10 in each round. Moreover, because base station is outside, the fitness function is constructed mainly based on inter-cluster distance. As can be seen from Fig. 5, cluster head is relatively close to the base station to avoid long distance transmission.
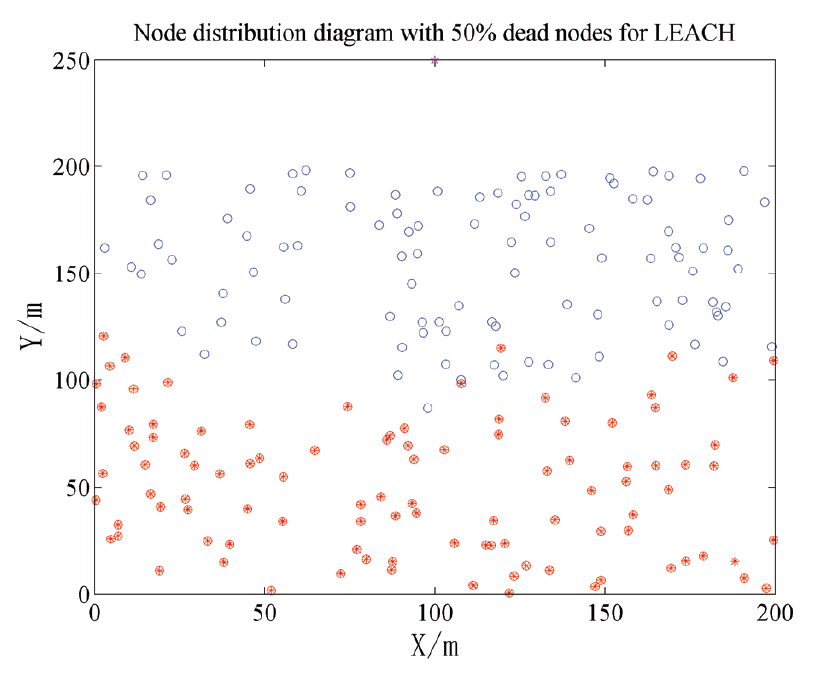
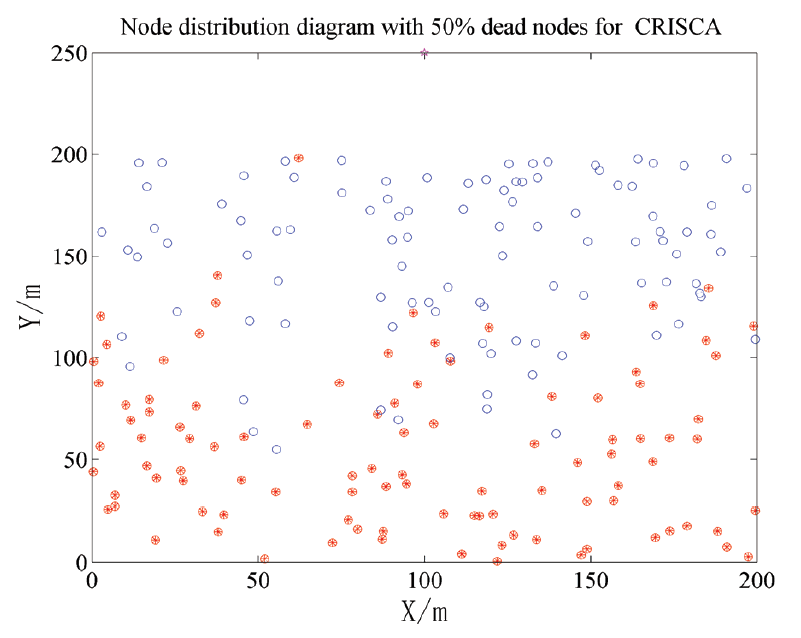
In Figs. 6 and 7, the dead nodes in LEACH and CRISCA are both at the bottom of region. These nodes die due to long distance transmission. Long distance transmission is not considered in the LEACH algorithm; in CRISCA, although the distance factor is taken into account when building the fitness function, the actual effect is not very ideal. In Fig. 8, the distribution of dead nodes is relatively uniform, because the improved algorithm constructs the fitness function with inter-cluster distance. In improved algorithm, cluster heads really play a role in avoiding long distance transmission.
Table 2.
| Proportion of death nodes | LEACH | CRISCA | Improved algorithm |
|---|---|---|---|
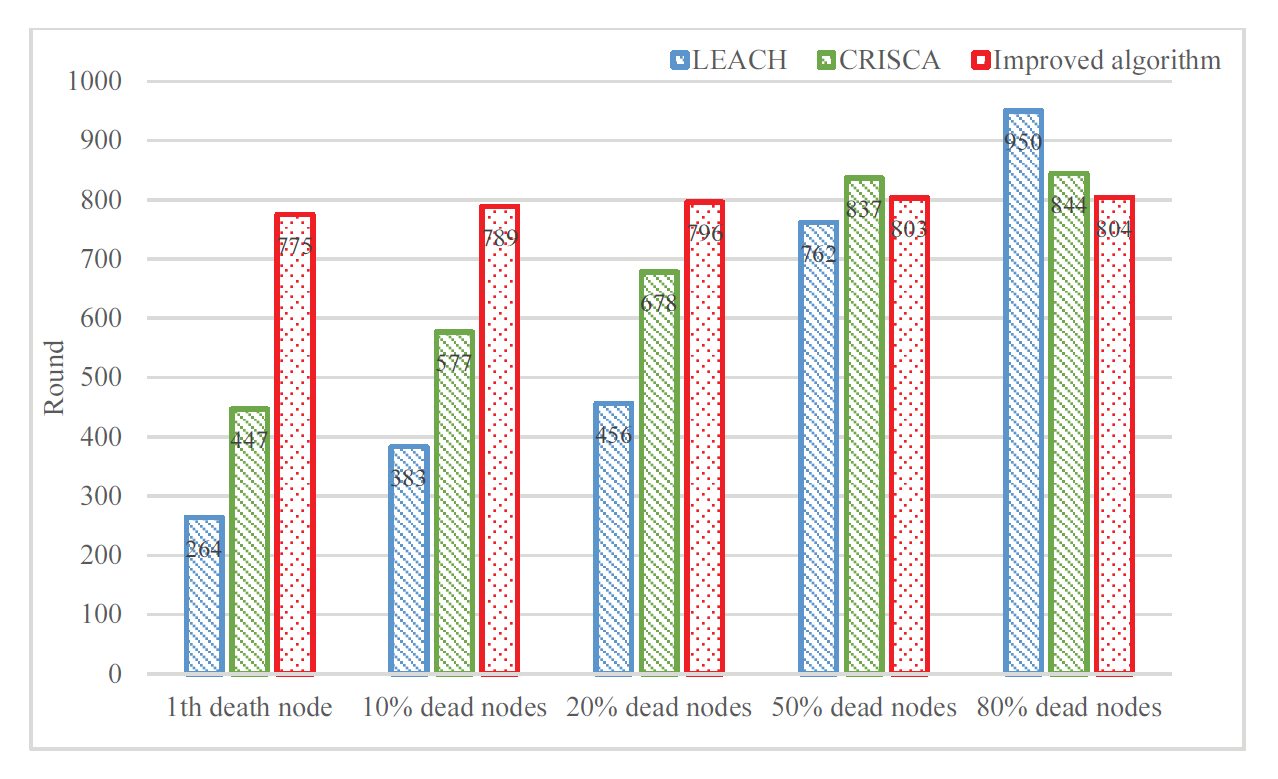
| 1st death node appears | 264 | 447 | 775 |
| 10% death nodes appear | 383 | 577 | 789 |
| 20% death nodes appear | 456 | 678 | 796 |
| 50% death nodes appear | 762 | 837 | 803 |
| 80% death nodes appear | 950 | 844 | 804 |
Occurrence of death nodes are greatly delayed in improved algorithm in Table 2 and Fig. 9. In LEACH the first dead node appears at 264th round, while it is at 775th round in improved algorithm, about 2.9 times than in LEACH. Moreover, the time of death of 10%, 20%, and 50% nodes in the improved algorithm are also delayed than that in LEACH and CRISCA. It only takes about 30 rounds from the first dead node to 80% dead nodes in improved algorithm. The 80% node death appears at 804th round in the improved algorithm, while that appears at the 950th and 844th round, respectively, in LEACH and CRISCA. Although there are some surviving nodes in them, there is a serious network segmentation in this region. Therefore, the significance of the existence of the network is not great.
In the paper, the distance between clusters is used to construct the fitness function, and the effect of distance on the balance of energy consumption is fully considered. In order to compare with the LEACH, CRISCA and the improved algorithm, the following scenarios are simulated in this paper, as shown in Table 3. Many simulation experiments have been carried out by changing the size of the monitoring area, the total number of nodes and the location of the base station. The average data of multiple runs are recorded. It can be seen that the first death node appearance in the improved algorithm occurs relatively late. The energy consumption is more balanced, and it only takes a short period from the first death node to 80% death nodes.
Table 3.
| Region | Node number | Base station coordinates | Algorithm | Round of death nodes | |
|---|---|---|---|---|---|
| 1st death node | 80% death nodes | ||||
| 200×200 | 200 | 100,250 | LEACH | 264 | 950 |
| CRISCA | 447 | 844 | |||
| Improved algorithm | 775 | 804 | |||
| 200×200 | 200 | 100,350 | LEACH | 103 | 519 |
| CRISCA | 289 | 380 | |||
| Improved algorithm | 337 | 391 | |||
| 100×100 | 100 | 50,150 | LEACH | 810 | 1157 |
| CRISCA | 1002 | 1079 | |||
| Improved algorithm | 1005 | 1021 | |||
| 100×100 | 100 | 50,250 | LEACH | 342 | 765 |
| CRISCA | 389 | 659 | |||
| Improved algorithm | 586 | 615 | |||
5.2.2 Energy balance
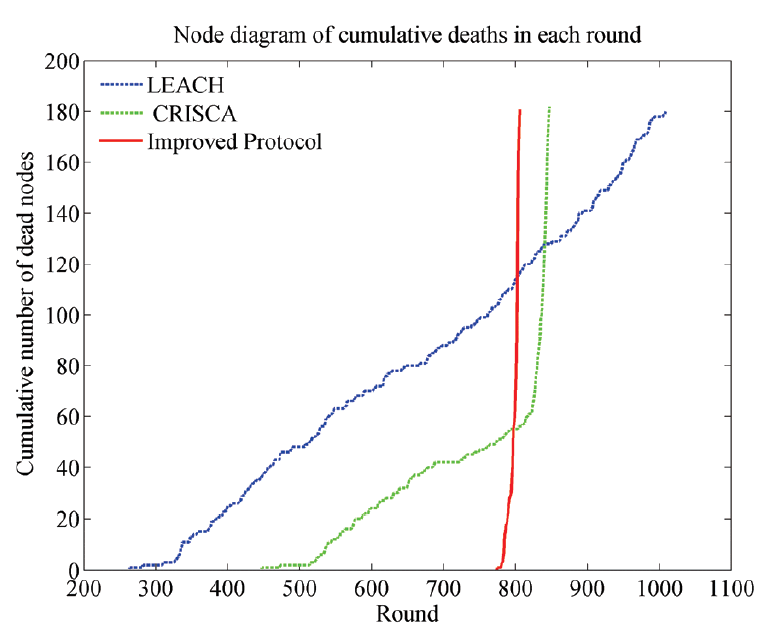
In Fig. 10, the death node of LEACH appears at about 260th round, that of CRISCA does at about 450th round, while that of improved algorithm appears much later, at about 770th round. Improved algorithm greatly prolongs the network life. Moreover, in improved algorithm, as soon as the first dead node appears, 80% of the nodes die quickly. It well balances energy consumption among nodes. About 80% of the dead nodes of LEACH algorithm appears at about 950th round. And 80% of the death nodes of CRISCA appears about at 844th round. The reason is that nodes far from base station die prematurely, thus remaining surviving nodes become closer to base station, resulting in delaying death time of these surviving nodes.
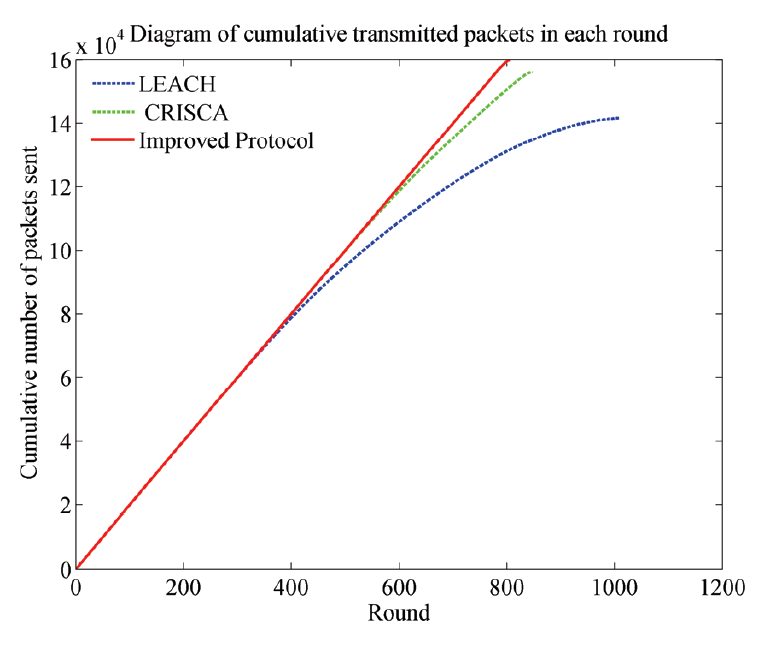
5.2.3 Throughput
In Fig. 11, the packets sent by improved algorithm is more than those by LEACH and CRISCA. Because appearing time of dead node in improved algorithm is delayed, survival time of whole network is prolonged, the time that all nodes can gather and transmit data becomes longer, and the total amount of data packets sent gets more. In addition, LEACH and CRISCA can continue sent data to base station after about 800th round, since there are some surviving nodes gathering and transmitting data in them.
6. Conclusion
From the perspective of prolonging network life cycle and balancing energy consumption, a new centralized clustering algorithm is proposed based on SCA in this paper. The algorithm determines the optimal number of cluster heads according to the current surviving node to adapt to the dynamic changes in network size. And the algorithm uses high-energy nodes to construct candidate cluster heads, and constructs fitness function according to the distance between clusters. Then, the algorithm uses SCA based on monotone decreasing convex function to find the optimal cluster head scheme with the lowest communication cost. The algorithm can well balance energy consumption among nodes to improve network energy utilization efficiency and throughput. And it can greatly postpone the rounds of death nodes to extend the effective life of the whole network. Moreover, compared with CRISCA algorithm, the fitness function of algorithm is much simpler and more efficient, and the burden on the base station gets lighter. The algorithm has better prospects in large-scale networks, but there are still some areas to be improved. In the following step, we will further study the layering or chain algorithm between clusters in a larger scale network deployment scenario.
Biography
Xinghua Sun
https://orcid.org/0000-0002-5636-1505He is working as a professor in School of Information Science and Engineering in Hebei North University, Zhangjiakou, China. He received M.S. degree in School of Mathematical Information in Shanghai Normal University in 2007. His current research interests include mobile communication and lighting control network.
Biography
Biography
Meng Liu
https://orcid.org/0000-0002-5338-6184She is currently working at the College of Information Science and Engineering, Hebei North University, Zhangjiakou, China. She received her master's degree in management from Beijing University of Chinese Medicine in 2020. Her main research interests are computer networks and information management.
References
- 1 W. R. Heinzelman, A. Chandrakasan, and H. Balakrishnan, "Energy-efficient communication protocol for wireless microsensor networks," in Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, 2000, pp. 3005-3014.doi:[[[10.1109/hicss.2000.926982]]]
- 2 D. Li and D. M. Xu, "Improvement of LEACH algorithm in wireless sensor networks," Computer Engineering and Design, vol. 41, no. 7, pp. 1852-1857, 2020.doi:[[[10.1109/SENSORCOMM.2007.4394931]]]
- 3 Y . F. Tian and L. H. Wang, "Routing algorithm for wireless sensor networks by considering residual energy and communication cost," Journal of Nanjing University of Science and Technology, vol. 42, no. 1, pp. 96101, 2018.custom:[[[-]]]
- 4 X. H. Li, Y . C. Zhao, and J. P . Zhao, "Poisson distribution optimal number of cluster heads in wireless sensor networks," Communications Technology, vol. 53, no. 2, pp. 335-340, 2020.custom:[[[-]]]
- 5 H. B. Li, Z. L. Liu, Q. Chen, S. Liu, X. L. Liu, Y . Q. Liang, Z. Yang, and L. W. Chen, "Clustering routing algorithm for wireless sensor network based on hierarchical neighboring nodes," Computer Engineering, vol. 46, no. 6, pp. 187-195, 2020.doi:[[[10.19678/j.issn.1000-3428.0054723]]]
- 6 J. Kim, D. Lee, J. Hwang, S. Hong, D. Shin, and D. Shin, "Wireless sensor network (WSN) configuration method to increase node energy efficiency through clustering and location information," Symmetry, vol. 13, no. 3, article no. 390, 2021. https://doi.org/10.3390/sym13030390doi:[[[10.3390/sym13030390]]]
- 7 Z. S. Wang, H. W. Ding, B. Li, H. Li, and A. S. Li, "Energy-efficient WSNs routing protocol based on clustering," Computer Engineering and Design, vol. 42, no. 2, pp. 324-330, 2021.custom:[[[-]]]
- 8 P . Maheshwari, A. K. Sharma, and K. V erma, "Energy efficient cluster based routing protocol for WSN using butterfly optimization algorithm and ant colony optimization," Ad Hoc Networks, vol. 110, article no. 102317, 2021. https://doi.org/10.1016/j.adhoc.2020.102317doi:[[[10.1016/j.adhoc..102317]]]
- 9 S. Sefati, M. Abdi, and A. Ghaffari, "Cluster-based data transmission scheme in wireless sensor networks using black hole and ant colony algorithms," International Journal of Communication Systems, vol. 34, no. 9, article no. e4768, 2021. https://doi.org/10.1002/dac.4768doi:[[[10.1002/dac.4768]]]
- 10 N. Ajmi, A. Helali, P . Lorenz, and R. Mghaieth, "MWCSGA—Multi weight chicken swarm based genetic algorithm for energy efficient clustered wireless sensor network," Sensors, vol. 21, no. 3, article no. 791, 2021. https://doi.org/10.3390/s21030791doi:[[[10.3390/s0791]]]
- 11 X. He, Z. Z. Ning, and X. Y . Yang, "WSN clustering routing protocol based on improved sine cosine algorithm," Journal of Xi'an University of Post and Telecom, vol. 26, no. 2 pp. 15-20, 2021.custom:[[[-]]]
- 12 S. Mirjalili, "SCA: a sine cosine algorithm for solving optimization problems," Knowledge-based Systems, vol. 96, pp. 120-133, 2016.doi:[[[10.1016/j.knosys.2015.12.022]]]
- 13 C. Chen, L. Ma, and Y . Liu, "Quantum sine cosine algorithm for function optimization," Application Research of Computers, vol. 34, no. 11, pp. 3214-3218, 2017.custom:[[[-]]]
- 14 L. Q. Yong, Y . H. Li, and W. Jia, "Literature Survey on Research and Application of Sine Cosine Algorithm," Computer Engineering and Applications, vol. 56, no. 14, pp. 26-34, 2020.custom:[[[-]]]
- 15 Y . Liu and L. Ma, "Sine cosine algorithm with nonlinear decreasing conversion parameter," Computer Engineering and Applications, vol. 53, no. 2, pp. 1-5, 2017.doi:[[[10.3778/j.issn.1002-8331.1608-0349]]]
- 16 D. Chen and Y . H. Zhao, "Speed control of permanent magnet synchronous motors using fuzzy PI controller based on sine cosine algorithm," Electric Drive, vol. 49, no. 5, pp. 31-36, 2019.doi:[[[10.1016/j.ijepes.2012.06.013]]]
- 17 P . S. Rao, P . Lalwani, H. Banka, and G. S. N. Rao, "Competitive swarm optimization based unequal clustering and routing algorithms (CSO-UCRA) for wireless sensor networks," Multimedia Tools and Applications, vol. 80, no. 17, pp. 26093-26119, 2021.doi:[[[10.1007/s11042-021-10901-4]]]
- 18 S. P . Su and H. j. Zhang, "Scheme of adaptive clustering based on optimal number of cluster nodes for WSNs," Control Engineering of China, vol. 24, no. 5, pp. 1070-1074, 2017.custom:[[[-]]]
- 19 K. S. Arikumar, V . Natarajan, and S. C. Satapathy, "EELTM: an energy efficient LifeTime maximization approach for WSN by PSO and fuzzy-based unequal clustering," Arabian Journal for Science and Engineering, vol. 45, no. 12, pp. 10245-10260, 2020.doi:[[[10.1007/s13369-020-04616-1]]]