Yanli Chu , Yuyao He , Junfeng Chen and Qiwu Wu
Non-uniform Weighted Vibration Target Positioning Algorithm Based on Sensor Reliability
Abstract: In the positioning algorithm of two-dimensional planar sensor array, the estimation error of time difference-of-arrival (TDOA) algorithm is difficult to avoid. Thus, how to achieve accurate positioning is a key problem of the positioning technology based on planar array. In this paper, a method of sensor reliability discrimination is proposed, which is the foundation for selecting positioning sensors with small error and excellent performance, simplifying algorithm, and improving positioning accuracy. Then, a positioning model is established. The estimation characteristics of the least square method are fully utilized to calculate and fuse the positioning results, and the non-uniform weighting method is used to correct the weighting factors. It effectively handles the decreased positioning accuracy due to measurement errors, and ensures that the algorithm performance is improved significantly. Finally, the characteristics of the improved algorithm are compared with those of other algorithms. The experiment data demonstrate that the algorithm is better than the standard least square method and can improve the positioning accuracy effectively, which is suitable for vibration detection with large noise interference.
Keywords: Error , Least Square Method , Non-uniform Weight , Sensor Reliability , TDOA Positioning
1. Introduction
Sensor vibration source positioning is widely used in both industrial and military fields. Due to the impact of natural environment and system noise, it is more appropriate to use planar array to locate the target in two-dimensional space, similar to passive positioning in inaccessible border monitoring [1]. At present, there are numerous researches on the target positioning technology of regular planar array (such as semi-cross array and cross array), but few on the non-uniform weighted positioning technology of arbitrary planar array [2]. Multi-station time difference-of-arrival (TDOA) has always been a hot topic in passive positioning research. At present, multi-sensor passive cooperative positioning algorithms [3] mainly include least squares algorithm, overall least squares algorithm, and other algorithms. But the above method is mostly applied in the multi-sensor measurement accuracy under the condition of the same or close. However, in the multi-sensor fusion [4], the effect of environmental variability and internal noise of the system, the sensor measurement value may be failure. If the general positioning algorithm is used, resulting from the fusion of target location accuracy will be a sharp drop in. In addition, the least squares method and weighted least squares method realize the target positioning based on the further transformation of the mathematical model of the signal arrival angle, It is inevitable that many errors will be brought in the process of formula transformation which will inevitably introduce many errors in the transformation process of the formula, and resulting in the reduction of the positioning accuracy of the least squares positioning and weighted least squares positioning. In [5], the double least square method is used to solve the positioning equations in a non-iterative closed form. This method has good estimation performance in the case of slight measurement error of TDOA. However, with the increase of measurement error, the performance of the algorithm will drop rapidly, which will affect the positioning accuracy [6]. In multi-sensor fusion, it is of great significance to reduce the influence of measurement error on target positioning accuracy, which is the premise of improving positioning accuracy.
Directly using TDOA algorithm to solve a set of hyperbolic equations established by each sensor to solve the target coordinate value, which can lead to low positioning accuracy. The uncertainty of measurement can be eliminated by the least square method, and the real-time measurement results are more reliable. However, the estimation accuracy of the least square method is not very high, because all sensors are selected regardless of advantages and disadvantages before using the least square method, and the measured values are used for average operation indiscriminately [7]. Solving a set of hyperbolic equations established by each sensor with the TDOA algorithm to obtain of judging sensor reliability is proposed to reduce the detection error, and then the least square method weighting is improved to ensure the improvement of positioning accuracy the target coordinates will lead to a low positioning accuracy. For the finite number of measurements, the arithmetic average method is usually used. Though this method improves the measurement results to some extent, it cannot satisfy the requirements of high-precision positioning [8]. The measurement uncertainty can be eliminated by the least square method [9], and the real-time measurement results are more reliable. However, the estimation accuracy of the least square method is not very high, because the sensors are selected without discrimination before the method is used, and the measured values are used indiscriminately for average calculation [10].
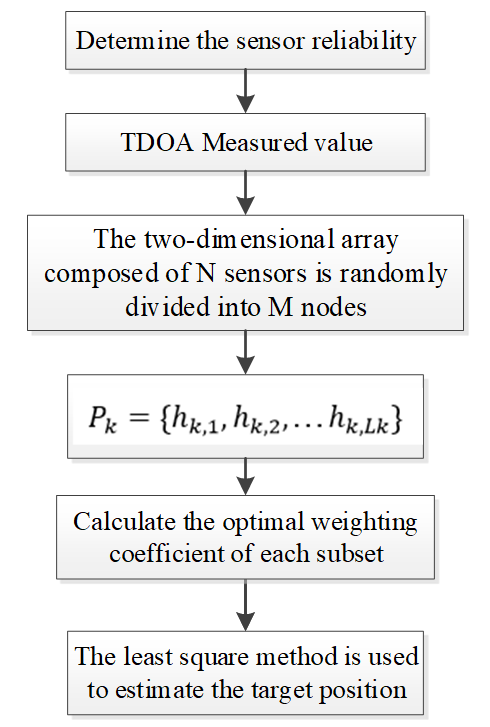
In this paper, an improved non-uniform weighting algorithm based on node-surface array is proposed. Firstly, a method to judge sensor reliability is proposed to reduce the detection error. Then, the planar sensor array of arbitrary shape is divided into several sub-planar arrays, and according to the sensor reliability, the sensor with high reliability is selected as the participating positioning sensor. Finally, the optimal weighting coefficient is calculated for the positioning results of each node, and then the positioning results of each sub-plane array are fused by data fusion technology. This method reduces the error of data processing caused by the average weighted and gives full play to the advantage of least square method.
The contributions of this paper are summarized as follows:
(1) A sensor reliability discrimination method based on signal characteristic parameters is proposed. By comparing the deviation of the characteristic parameters of each signal from the center value, the reliability of the sensor is identified. This method lays a foundation for the subsequent selection of the positioning sensor with small error and excellent performance, the algorithm is simplified and the positioning accuracy is improved.
(2) An optimal weighting coefficient calculation method based on sensor reliability is proposed. For sensors with different reliability, the method of Lagrange extremum is used to construct auxiliary functions and obtain the optimal weighting coefficients. This method improves the method of directly calculating the mean value by using the measured data regardless of advantages and disadvantages.
(3) A non-uniform weighted positioning algorithm based on sensor reliability is proposed. For multiple sensors, select some of these sub-sets, establish the positioning model, and construct the hyperbolic equation for each subset to solve the target location. We fully use the estimation characteristics of the least squares method to calculate the positioning results, and the weighted factors are corrected by the optimal weighted coefficient. The problem of the accuracy of the positioning accuracy is solved effectively, and the performance of the algorithm is greatly improved.
2. Related Work
The positioning algorithm is generally studied based on iterative and analytical methods. Iterative positioning solutions include maximum likelihood estimation method [10], quadratic constraint method [11], single station TDOA positioning algorithm based on constrained population least squares [12], and constrained weighted least squares (CWLS) [13]. The iterative positioning method cannot converge to the global optimal solution if the initial value selection is not ideal, and the complexity of the algorithm is high because of several iterations. However, analytical methods need no iteration and have low computational complexity. The famous two-stage weighted least squares (TSWLS) [14] is one of the representatives of this method. However, although the computational complexity of this method is low when the noise of the TDOA algorithm is high, the positioning deviation is large. The positioning accuracy will deviate from the Cramer-Rao lower bound (CRLB). Taken together, the two kinds of methods of their respective defects. How to be in a higher noise environment, and under the premise of without increasing the complexity of algorithm, the positioning accuracy can still close to CRLB is a problem that is urgently needed. In [15], for the problem put forward a non-source positioning method based on positioning error correction is proposed. Its positioning accuracy is improved without increasing the complexity of the algorithm. But when the noise increases, the positioning accuracy deviates from CRLB. In [16], a TDOA/FDOA sequence quadratic program (SQP) positioning algorithm is proposed. This algorithm can achieve CRLB when the noise is high, but it needs to be iterated several times due to the introduction of SQP method, and the algorithm complexity is high. In [17], an improved time difference and frequency difference joint location algorithm of CWLS is proposed. This algorithm improves the positioning accuracy in low noise environment, and the algorithm does not need iteration. However, its positioning accuracy still cannot achieve CRLB in high noise condition.
In [18], uses multi-node direction finding information based on the least square method for target positioning, but it is only applicable to two-dimensional targets. In [19], Taylor series expansion is used to transform the nonlinear system into a linear system, and the measurement errors of each platform are introduced into the estimation equation as weights, then the least square method is used for positioning. Its disadvantage is that the high-order characteristics in the nonlinear observation equation are ignored, so the positioning accuracy is not high. From the perspective of nonlinear estimation, Fu et al. [20] proposed the least squares estimation algorithm based on Newton iteration, which retained the observation error of the second order or even higher order, improved positioning accuracy and the stability of the positioning results, but only gave the results in the two-dimensional plane. Jin et al. [21] deduced the least squares target positioning method based on Angle information in 3D space, and tried to integrate TDOA and DOA modal information to improve positioning performance. However, the tangent value of pitch Angle needs to be calculated in the least squares solution, and due to the highly nonlinear tangent function around 90°, small Angle estimation error leads to large tangent value error. It will eventually lead to the rapid degradation of positioning performance when some nodes are located at the same or close depth to the target.
Although these methods differ in performance and computational complexity, they have a common feature—they all aim to reduce noise interference and improve accuracy in measured data. The non-uniform weighted positioning algorithm based on least square method is studied for arbitrary planar sensor array, and a set of hyperbolic equation established by each sensor is solved by TDOA algorithm to solve the target coordinate value. Since TDOA estimation error is difficult to avoid, how to achieve accurate positioning is the core problem of planar array positioning technology. In this paper, an algorithm combining sensor reliability with non-uniform weighted least square method is introduced. The method of judging sensor reliability is proposed to reduce the detection error, then through the non-uniform weighting method. the weighting factor is corrected to reduce the data processing error caused by the average weighting for positioning orientation. The algorithm gives full play to the advantages of the least square method to effectively ensure the improvement of positioning accuracy.
3. Sensor Reliability
Characteristic parameter analysis of the received signal is one of the key technologies of signal processing [22]. In the multi-sensor multi-node joint positioning system, the ability of each sensor to receive a vibration source signal can be described by the characteristic parameters of the signal. An effective signal processing method can accurately extract the information that can reflect the characteristics of the vibrating target, provide a reliable basis for judging the quality of the signal, and improve the positioning efficiency effectively [23].
For the same vibration source, the characteristic parameters of the signals received by each sensor are similar during the same period of time. By comparing the deviation of the characteristic parameters of each signal from the central value, the advantages and problems of each sensor in receiving the current vibration target signal can be determined. Thus, the signals collected by sensors with good receiving effect are selected as the positioning parameters.
Suppose there are n vibration sensors in a system, the signals received by each sensor have m characteristic parameters, and [TeX:] $$P_i(j)$$ is the jth characteristic parameter of the [TeX:] $$i^{\text {th }}$$ sensor. Then, the average value (characteristic parameter reference value) of the [TeX:] $$j^{\text {th }}$$ characteristic parameter of the n sensors is [TeX:] $$P_i(j)$$ [TeX:] $$i=0,1, \ldots n-1,$$ where [TeX:] $$\delta_i(j)$$ indicates the deviation of the [TeX:] $$i^{\text {th }}$$ sensor’s characteristic parameter to the reference value.
For convenience of data processing, [TeX:] $$\delta_i(j)$$ is mapped to the range of 0-1, and we perform the normalization method to obtain the deviation distance:
The normalized distance sum [TeX:] $$S_i$$ of m characteristic parameters of the [TeX:] $$i^{\text {th }}$$ sensor is:
The normalized distance sum of the m characteristic parameters of the [TeX:] $$i^{\text {th }}$$ sensor can be obtained by the same method, which is called sensor reliability [TeX:] $$\left(\lambda_i\right),$$ or the reliability of the [TeX:] $$i^{\text {th }}$$ sensor:
The larger the value of , the closer the detected signal characteristics to the center value of the reference characteristic, which means the signals collected by the sensor is good in quality.
4. Planar Array Positioning Model
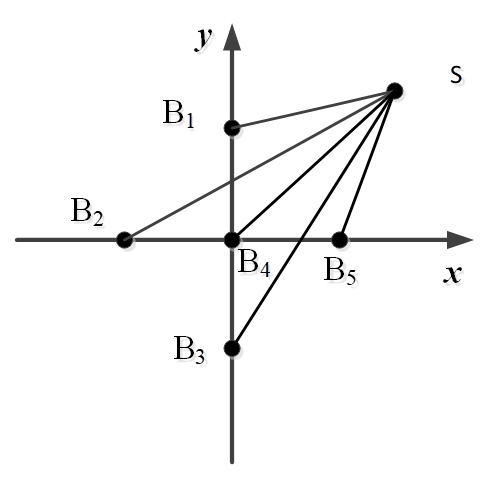
In the two-dimensional plane, it is assumed that the detection array has [TeX:] $$n(n \geq 3)$$ non-collinear receiving sensors to participate in target positioning. As shown in Fig. 1, its coordinates are [TeX:] $$B_i\left(x_i, y_i\right)(i=0,1,2, \ldots, n-1),$$ and the distance from the vibration source to the [TeX:] $$i^{\text {th }}$$ sensor is [TeX:] $$r_i(i=0,1,2, \ldots, n-1) .$$ Let the traveling speed of vibration signal be c, the time difference between the vibration source to the [TeX:] $$i^{\text {th }}$$ sensor and the source to the [TeX:] $$0^{\text {th }}$$ sensor be [TeX:] $$\tau_{i0}$$, and the distance difference between the vibration source to the [TeX:] $$i^{\text {th }}$$ sensor and the source to the [TeX:] $$0^{\text {th }}$$ sensor be [TeX:] $$r_{i 0}$$, and we have [TeX:] $$r_{i, 0}=r_i-r_0.$$ Let the actually measured distance difference [TeX:] $$r_{i 0}$$ of multiple sensors be [TeX:] $$r_{i 0}=\left(r_{10}, r_{20}, \ldots, r_{n-10}\right)$$.
Then, n-1 positioning equations can be established: [TeX:] $$r_{i, 0}=c \tau_{i 0}=r_i-r_0.$$
where
The above equation is actually composed of n-1 equations. Transforming the equation set into matrix form, we have
where,
The least square method is used to obtain the initial position:
A solution of the target position can be obtained by selecting three non-collinear sensors from the set of sensors involved in the positioning. The error between the position coordinates and the actual coordinates of the vibration source depends on the accuracy of the measurement delay difference of the sensors participating in the positioning. When the time delay estimation algorithm is known, the accuracy of the time delay difference is determined by the signal quality of the sensor [25]. The sensor with good signal quality has a smaller error, and its positioning accuracy will be higher.
According to the reliability of each characteristic parameter of each sensor obtained from Eq. (3), two of n-1 equations with high reliability are selected and solved, and the optimal estimated coordinates [TeX:] $$\left(x_1, y_1\right)$$ of vibration source can be obtained. The estimated coordinates of i positions [TeX:] $$\left(x_i, y_i\right)(1 \leq i \leq m)$$ can be obtained by selecting i groups of three non-collinear sensors in combination with sensor reliability, and [TeX:] $$(\bar{x}, \bar{y})$$ can be obtained by the weighted average method.
5. Node Non-uniform Weighting Method
The environmental noise and TDOA measurement error has great impact on the weighted least square method [26]. Therefore, we randomly divide the two-dimensional array composed of n sensors into m nodes, and each node consists of several sensors. According to Eq. (3), the reliability of each sensor is determined, and the sensor with high reliability is selected to participate in the positioning. Then the positioning results of each node are weighted and averaged. We select [TeX:] $$L(3 \leq L \leq n)$$ unrelated sensors from the set of receiving sensors to construct the [TeX:] $$k^{\text{th}}$$ node, and obtain a subset:
Given the number of sensors ([TeX:] $$L_k$$) in a node, each subset [TeX:] $$P_k$$ has [TeX:] $$C_N^{L k}$$ possibilities. Obviously, increasing the subset number of weighted average is the premise to reduce the sample variance of positioning error, but it will result in unnecessary calculations. To reduce the amount of calculation, we can choose m subsets, and construct hyperbolic equations for each subset [TeX:] $$P_k$$ to solve the target position [TeX:] $$P_k(k=1,\ldots,m)$$. In this way, the total error of the solution of each subarray can be optimized. When the error is less than the TDOA measurement error, each subarray can be weighted, and the solution of the weighting coefficient is as follows:
(10)
[TeX:] $$\text { Let } \Psi=\sum_{i=1}^m \lambda_i \sigma_i^2=\sum_{i=1}^m\left[\lambda_i\left(x-x_i\right)^2+\lambda_i\left(y-y_i\right)^2\right] \text {. }$$Let [TeX:] $$\frac{\partial \Psi}{\partial x}=0, \frac{\partial \Psi}{\partial y}=0.$$
We can obtain
(11)
[TeX:] $$x=\frac{\lambda_1 x_1+\lambda_2 x_2+\cdots+\lambda_m x_m}{\lambda_1+\lambda_2+\cdots+\lambda_m}=\sum_{i=1}^m k_i x_i,$$
(12)
[TeX:] $$y=\frac{\lambda_1 y_1+\lambda_2 y_2+\cdots+\lambda_m y_m}{\lambda_1+\lambda_2+\cdots+\lambda_m}=\sum_{i=1}^m k_i y_i,$$where
The value of [TeX:] $$k_i$$ can be measured by prior experiments. In order to improve the performance of the algorithm, the estimated value of [TeX:] $$k_i$$ is corrected by the non-uniform weighting method. In order to obtain the optimal weighting coefficient, Lagrange method is adopted to find the extreme value, and an auxiliary function is constructed as follows:
(14)
[TeX:] $$f\left(k_1, k_2, \ldots, k_n, \eta\right)=\sum_{i=1}^n k_i^2 d_i^2-\eta\left(\sum_{i=1}^n k_i-1\right),$$where [TeX:] $$d_i^2=\left(\bar{x}-x_i\right)^2+\left(\bar{y}-y_i\right)^2$$
Accordingly, an equation set can be established:
(15)
[TeX:] $$\left\{\begin{array}{c} \frac{\partial f}{\partial k_1}=2 k_1 d_1^2-\eta=0 \\ \frac{\partial f}{\partial k_2}=2 k_2 d_2^2-\eta=0 \\ \vdots \\ \frac{\partial f}{\partial k_n}=2 k_n d_n^2-\eta=0 \end{array}\right.,$$
By solving the equations, we get:
It can be seen from Eq. (15) that the sensor with small error has a large weight, and its collected data accounts for a high proportion in the weighted estimation value. On the contrary, the sensor with large error has a small weight, which accounts for a low proportion in the weighted estimation value. By comparing the weights, the method of averaging the measured data directly is improved.
The algorithm flowchart of this paper is as shown in Fig. 2.
6. Simulation Experiment
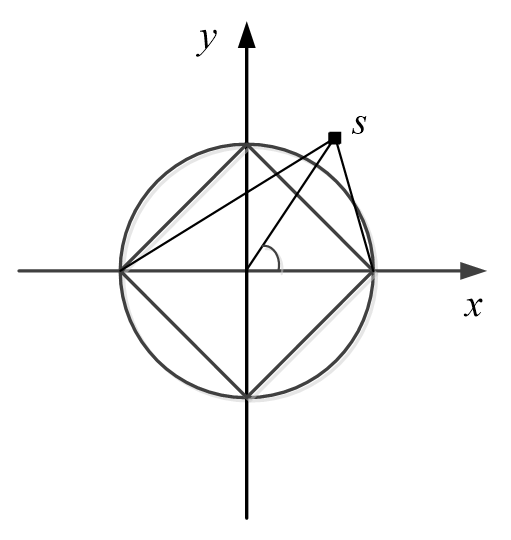
In order to verify the effectiveness of the algorithm, we tested the algorithm, the average weighting method and Newton iteration method, respectively, and the statistical results of the three methods are compared. By using the biased estimation method, the performance evaluation criteria are expressed by the average positioning and orientation error. The hardware environment of the simulation experiment part is Intel Xeon E5 as CPU, with 32 GB memory. The software environment is Windows 7 platform and MATLAB 2022a.The sensor array selected is a five-element cross array, which forms a circle with a radius of 10m. The coordinate system is established as shown in Fig. 3.
Let the vibration signal speed be c = 140 m/s, the measured TDOA is its real value plus the zero-mean value, and the variance [TeX:] $$\sigma_{ms}$$ is obtained by the white noise sequence. Here, let [TeX:] $$\sigma_{ms}=0.05m$$, and the variance [TeX:] $$\sigma_{ms}$$, of TDOA measurement error is [TeX:] $$357 \mu s .$$
The five-element cross array can be regarded as a combination of eight isosceles right-angled triangular arrays and two linear arrays [2]. For the isosceles right-angle triangle array, we have:
where
(21)
[TeX:] $$b=\frac{\left(\Delta l_{12}-\Delta l_{13}\right)\left(d^2+\Delta l_{12} \Delta l_{13}\right)}{2 d \Delta l_{12}} .$$For the linear array, we have:
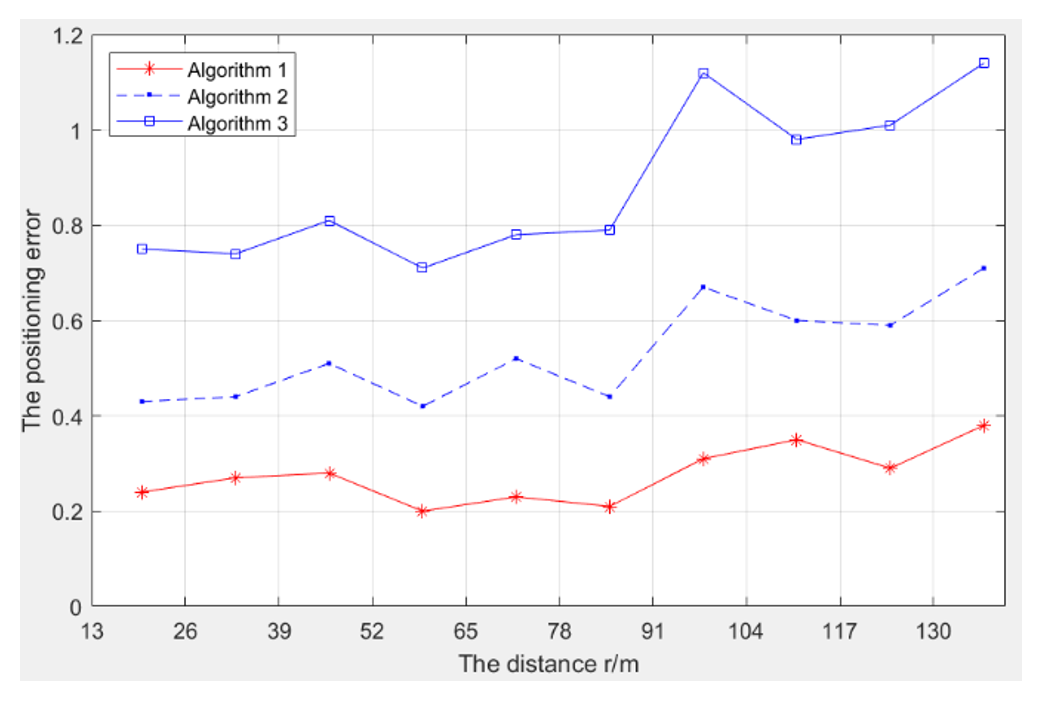
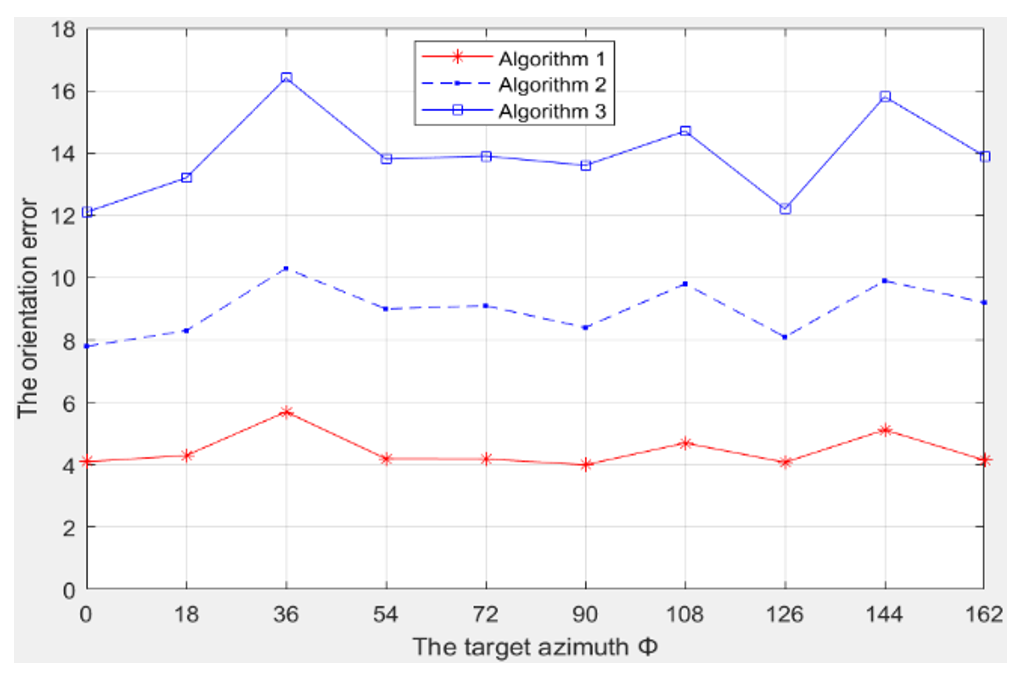
Let 1 be node subarray nonuniform weighting method, 2 the Newton iteration method, and 3 the weighted least square method. The target azimuth is [TeX:] $$\Phi=\pi / 4$$, and the distance between the vibration source and the origin (r) varies from 20 m to 100 m. When applying algorithm 1, M=10 subarrays are selected, and each subarray has [TeX:] $$L_k=5(k=1, \cdots, 4)$$ arbitrarily different sensors. For near-field targets, when r varies from 20m to 100m, the positioning error curve is shown in Fig. 4.
When r = 50 m, the error of [TeX:] $$\varphi$$ is shown in Fig. 4.
As can be seen from Figs. 4 and 5, for near-field targets, the sample positioning accuracy of Algorithm 1 is improved, its curve is stable, and the performance of standard deviation suppression and noise suppression is the best.
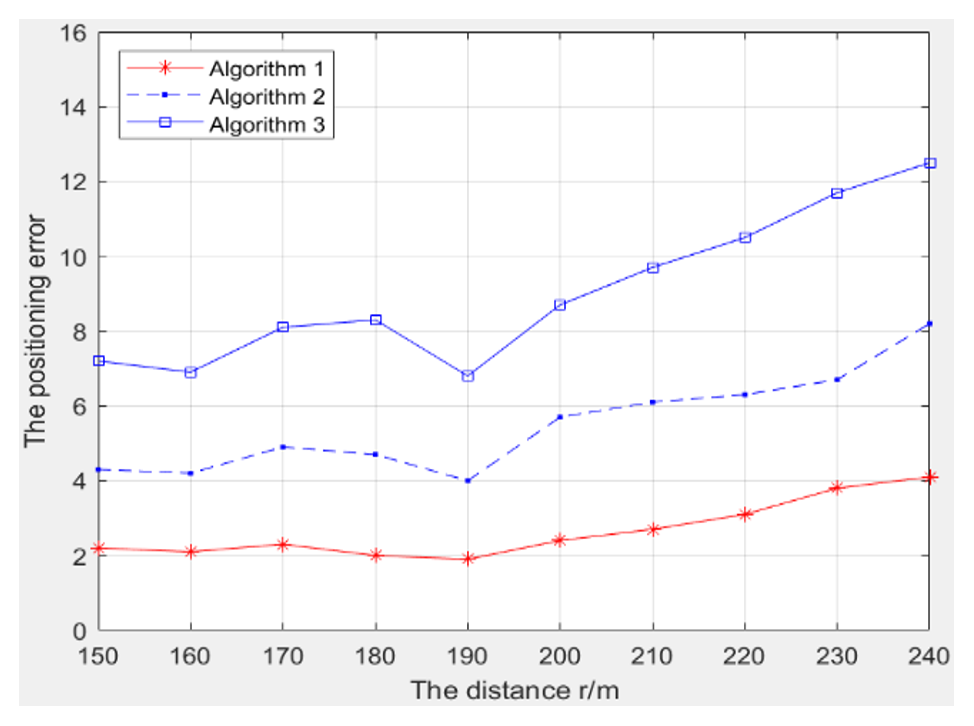
For far-field experimental targets, the distance between the vibration source and the origin is more than 10 times the array aperture. Let [TeX:] $$\Phi=\pi / 6$$, and the positioning error curve is shown in Fig. 6.
As can be seen from Fig. 5, the sample deviations of these algorithms are quite different for far-field vibration source targets. Algorithm 1 is superior to Algorithms 2 and 3 in standard variance of samples, and the root mean square error of r is the smallest. In addition, experiments demonstrate that the positioning accuracy of the target decreases with increased distance between the target and the center.
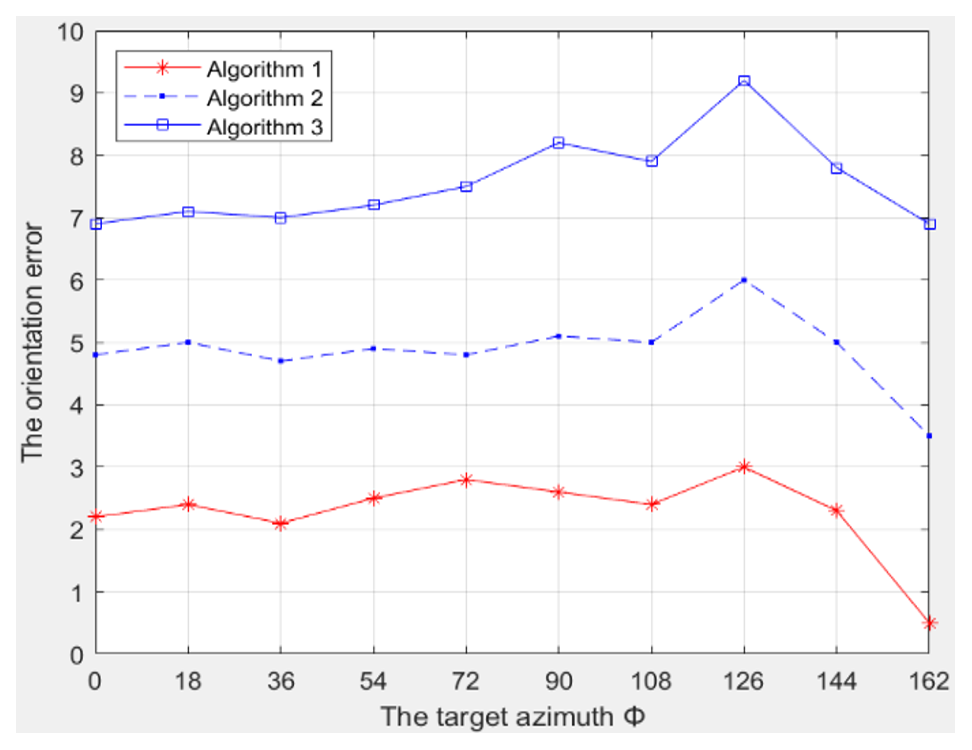
As can be seen from Fig. 7, for far-field vibration source targets, the target orientation accuracy of Algorithm 1 is much higher than that of Algorithms 2 and 3. When r=200, the orientation error ranges of the algorithms are 2 m, 4 m, and 6 m, respectively.
7. Conclusion
Based on the research on positioning of arbitrary shape area array, the sensor with superior performance is introduced to reduce the accumulated measurement error. Then, a non-uniform weighted least square algorithm is proposed, which reduces the error of data processing due to average weighting and gives full play to the advantages of the least square algorithm. The simulation results reveal that the improved algorithm is superior to the traditional least square method and Newton iteration method in near and far field positioning. It reduces the impact of TDOA measurement error and environment noise on the target positioning accuracy. At present, the joint positioning of multi-sensor has begun to be popular. In the further research work, photoelectric sensors, meteorological sensors and other types of sensors should be added to improve the positioning accuracy and enhance the adaptability of the positioning system. With the enhanced understanding of the detected parameters characteristics, and by processing the sample data, the characteristics of data collection are reflected from different angles, and the optimization of data processing is realized.
Biography
Biography
Biography
Biography
References
- 1 Y . He, Y . Chu, and S. Guo, "One-dimensional search location algorithm based on TDOA," Journal of Information Processing Systems, vol. 16, no. 3, pp. 639-647, 2020. https://doi.org/10.3745/JIPS.04.0172doi:[[[10.3745/JIPS.04.0172]]]
- 2 Y . Wang, M. Ni, and Y . Hu, "Improved localization algorithm based on planar array," Journal of Data Acquisition & Processing, vol. 2009, no. 2, pp. 198-202, 2009.custom:[[[-]]]
- 3 F. Jiang and Z. Zhang, "An improved underwater TDOA/AOA joint localisation algorithm," IET Communications, vol. 15, no. 6, pp. 802-814, 2021. https://doi.org/10.1049/cmu2.12122doi:[[[10.1049/cmu2.1]]]
- 4 A. Noroozi and M. A. Sebt, "Algebraic solution for three-dimensional TDOA/AOA localisation in multipleinput–multiple-output passive radar," IET Radar , Sonar & Navigation, vol. 12, no. 1, pp. 21-29, 2018. https://doi.org/10.1049/iet-rsn.2017.0117doi:[[[10.1049/iet-rsn.2017.0117]]]
- 5 J. Zhang, B. Tang, and F. Qin, "Application of Chan location algorithm in 3-dimensional space location," Computer Simulation, vol. 26, no. 1, pp. 323-325, 2009.custom:[[[-]]]
- 6 B. Friedlander, "Localization of signals in the near-field of an antenna array," IEEE Transactions on Signal Processing, vol. 67, no. 15, pp. 3885-3893, 2019. https://doi.org/10.1109/TSP .2019.2923164doi:[[[10.1109/TSP.2019.2923164]]]
- 7 S. Hara, D. Anzai, T. Yabu, K. Lee, T. Derham, and R. Zemek, "A perturbation analysis on the performance of TOA and TDOA localization in mixed LOS/NLOS environments," IEEE Transactions on Communications, vol. 61, no. 2, pp. 679-689, 2013. https://doi.org/10.1109/TCOMM.2013.012313.110509doi:[[[10.1109/TCOMM.2013.012313.110509]]]
- 8 J. W. Howse, L. O. Ticknor, and K. R. Muske, "Least squares estimation techniques for position tracking of radioactive sources," Automatica, vol. 37, no. 11, pp. 1727-1737, 2001. https://doi.org/10.1016/S00051098 (01) 00134-0doi:[[[10.1016/S00051098(01)00134-0]]]
- 9 Z. H. Qian and D. Y . Sun, "A survey on localization model in wireless networks," Chinese Journal of Computers, vol. 39, no. 6, pp. 1237-1256, 2016.custom:[[[-]]]
- 10 D. Huang, Y . Zhao, Y . Zhao, and M. Chu, "An algebraic solution for single-observer passive coherent location using DOA-TDOA-FDOA measurements," Journal of Electronics & Information Technology, vol. 43, no. 3, pp. 735-744, 2021. http://dx.doi.org/10.11999/JEIT200470doi:[[[10.11999/JEIT70]]]
- 11 S. Li, H. Sun, and H. Esmaiel, "Underwater TDOA acoustical location based on majorization-minimization optimization," Sensors, vol, 20, no. 16, article no. 4457, 2020. https://doi.org/10.3390/s20164457doi:[[[10.3390/s4457]]]
- 12 Y . Zou and H. Liu, "TDOA localization with unknown signal propagation speed and sensor position errors," IEEE Communications Letters, vol. 24, no. 5, pp. 1024-1027, 2020. https://doi.org/10.1109/LCOMM.2020. 2968434doi:[[[10.1109/LCOMM.2020.2968434]]]
- 13 Z. Gong, C. Li, and F. Jiang, "Passive underwater event and object detection based on time difference of arrival," in Proceedings of 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, 2019, pp. 1-6. https://doi.org/10.1109/GLOBECOM38437.2019.9014020doi:[[[10.1109/GLOBECOM38437.2019.9014020]]]
- 14 E. Dubrovinskaya and P . Casari, "Underwater direction of arrival estimation using wideband arrays of opportunity," in Proceedings of OCEANS 2019-Marseille, Marseille, France, 2019, pp. 1-7. https://doi.org/ 10.1109/OCEANSE.2019.8867262doi:[[[10.1109/OCEANSE.2019.8867262]]]
- 15 Y . Sun, Y . Y uan, Q. Xu, C. Hua, and X. Guan, "A mobile anchor node assisted RSSI localization scheme in underwater wireless sensor networks," Sensors, vol. 19, no. 20, article no. 4369, 2019. https://doi.org/ 10.3390/s19204369doi:[[[10.3390/s1969]]]
- 16 F. Qu, S. Wang, Z. Wu, and Z. Liu, "A survey of ranging algorithms and localization schemes in underwater acoustic sensor network," China Communications, vol. 13, no. 3, pp. 66-81, 2016. https://doi.org/10.1109/ CC.2016.7445503doi:[[[10.1109/CC.2016.7445503]]]
- 17 Y . S. Zhao, D. X. Shao, Y . J. Zhao, and C. Zhao, "Single-observer TDOA-FDOA location based on constrained total least squares," Electronic Warfare Technology, vol. 2016, no. 6, pp. 1-7, 2016.custom:[[[-]]]
- 18 J. Xu and L. Xue, "LS algorithm used in DF and localization," Chinese Journal of Radio Science, vol. 16, no. 2, pp. 227-230, 2001.custom:[[[-]]]
- 19 Z. Ni, G. Feng, and B. Ma, "An algorithm of multiple-vessel localization based on weighting least squares," Transactions of Beijing institute of Technology, vol. 2005, no. 11, pp. 971-974, 2005.custom:[[[http://journal.bit.edu.cn/zr/en/article/id/20051108]]]
- 20 S. Fu, X. Kong, Z. Li, and J. Li, "Bearing-only target cross location of multi-station based on nonlinear least squares," Fire Control & Command Control, vol. 34, no. 8, pp. 80-83, 2009.custom:[[[-]]]
- 21 L. Jin, H. Liang, and Y . Ma, "Target localization of UWSAN based on multi-modal information fusion," Journal of Northwestern Polytechnical University, vol. 35, no. 6, pp. 1020-1025, 2017.custom:[[[-]]]
- 22 Y . Chu, L. He, and F. Yao, "An improved localization algorithm of Taylor series expansion search target," Optik, vol. 127, no. 19, pp. 8070-8075, 2016. https://doi.org/10.1016/j.ijleo.2016.05.084doi:[[[10.1016/j.ijleo.2016.05.084]]]
- 23 S. Liu, M. Hu, J. Forrest, and Y . Yang, "Progress of grey system models," Transactions of Nanjing University of Aeronautics and Astronautics, vol. 29, no. 2, pp. 103-111, 2012.custom:[[[https://www.researchgate.net/publication/264950217_Progress_of_grey_system_models]]]
- 24 Y . Zhu and L. Feng, "Research on more nodes collocation excitation source based on Newton iterative method," Chinese Journal of Sensors and Actuators, vol. 2011, no. 9, pp. 1322-1325, 2011.custom:[[[https://www.researchgate.net/publication/293345684_Research_on_more_nodes_collocation_excitation_source_based_on_newton_iterative_method]]]
- 25 L. Feng and Y . Fan, "Taylor’s series expansion search vibratory source localization algorithm based on the gross error gray discriminant," Journal of Northwest Normal University (Natural Science), vol. 11, no. 6, pp. 49-53, 2014.custom:[[[-]]]
- 26 M. Wax and A. Adler, "Localization of multiple sources in the presence of model errors by total least squares," IEEE Transactions on Aerospace and Electronic Systems, vol. 57, no. 3, pp. 1949-1955, 2021. https://doi.org/10.1109/TAES.2020.3040538doi:[[[10.1109/TAES.2020.3040538]]]
- 27 X. Zhi, W. Wang, and Q. Liu, "Study on the location of the vibratory object on ground by regular triangle array," Journal of Detection & Control, vol. 8, no. 4, pp. 27-29, 2006.custom:[[[-]]]