Jun Cao
Image Enhancement Algorithm and its Application in Image Defogging
Abstract: An image enhancement algorithm and image defogging method are studied in this paper. The formation of fog and the characteristics of fog image are analyzed, and the fog image is preprocessed by histogram equalization method; then the additive white noise is removed by foggy image attenuation model, the atmospheric scattering physical model is constructed, the image detail characteristics are enhanced by image enhancement method, and the visual effect of defogging image is enhanced by guided filtering method. The proposed method has a good defogging effect on the image. When the number of training iterations is 3,000, the peak signal-to-noise ratio of the proposed method is 43.29 dB and the image structure similarity is 0.9616, indicating excellent image defogging effect.
Keywords: Atmospheric Scattering Physical Model , Guided Filtering , Histogram Equalization , Image Defogging , Image Enhancement
1. Introduction
In the field of deep learning, some scholars use different algorithms to enhance the image effect and resolution, and have achieved considerable economic benefits [1]. Affected by illumination, the image quality obtained by traditional cameras is not high. Lack of light is the primary difficulty in taking clear pictures. Even under the condition of artificial light source, it is easy to distort the image and make the color of the object more inclined to the color of the light source [2]. China's road traffic network is very developed. Relying on video monitoring and image processing, traffic congestion and illegal behaviors can be quickly recorded and handled to improve road traffic efficiency and driving safety; In the construction field, by placing monitoring equipment in different directions, the construction progress can be controlled at any time and the construction direction can be adjusted in time; In the field of security, the monitoring of high-risk areas and people allows for timely detection and prediction, and provides scientifically valid evidence [3].
As the visibility of people's image becomes higher and higher in the weather, the visibility of people's image is more and more contradictory to the fog [4,5]. Therefore, Image demisting technology has received more attention, and its application effect is good. In this paper, the image defogging will be further studied to obtain a clearer image. Therefore, it is very necessary to study the theoretical basis of image defogging.
You et al. [6] put forward a polarization image defogging enhancement algorithm on the basis of the a priori principle of dark channel, collected polarization images, extracted polarization features, and calculated polarization degree and polarization angle. The region growth algorithm is used to automatically extract the sky region, estimate the atmospheric light parameters of the sky region, and obtain the parameters related to the degree and angle of polarization of atmospheric light. Combined with the a priori dark channel principle, the atmospheric light intensity at infinity is obtained and the atmospheric light intensity of each pixel is calculated. Using the atmospheric physical degradation model, image defogging and enhancement are realized. However, the information entropy of this method is low. He et al. [7] proposed an image defogging method using the MALLAT algorithm, which converts the foggy image into a gray image, decomposes the gray image once by using two-dimensional discrete wavelet transform, processes the low-frequency sub image by gray linear transform, and processes the three high-frequency sub images by gray nonlinear transform. Wang et al. [8] presented a MSRCR image defogging algorithm based on multi-scale detail optimization. However, the peak signal-to-noise ratio is not high.
To solve the above problems, an image enhancement algorithm for image defogging is proposed in this work. Under the effect of guided filtering, each pixel in the guided image and the image to be filtered is traversed, and the image defogging is more refined, which helps to improve the image defogging quality.
2. Fog Image Preprocessing
2.1 Formation of Fog and Characteristics of Fog Image
There is a type of fog formed by radiation cooling, known in meteorology as radiation fog. It usually occurs during the night and early morning when there is a large temperature difference, or in sunny and breezy weather with abundant and stable water vapor near the ground. On the other hand, as the air passes over water or cold ground, the water vapor in the air is gradually cooled and liquefied to form fog. This is part of the horizontal movement of warm, moist air, known in meteorology as advection fog [9].
According to research, the reasons for the formation of fog include changes in humidity and temperature, and condensation nodules formed by particles in the atmosphere [10]. Firstly, in the atmospheric space close to the ground, the high humidity in the air promotes the condensation of water vapor in the atmosphere. In addition, the amount of water vapor that can be held in the atmosphere increases with temperature, which accelerates the condensation of water vapor. At a certain temperature, when the water vapor in the atmosphere is saturated, the excess water vapor will condense [11,12].
2.2 Histogram Equalization of Foggy Image
At present, the defogging algorithm based on image enhancement includes histogram equalization and other methods. This kind of algorithm is mainly to improve the contrast and saturation of the image, improve the color deviation and distortion, so as to achieve the purpose of image defogging. Although, it has been widely used in image defogging. However, this method does not remove the fog from the image at the source, losing the details of the image, and the defogging effect is not ideal. Therefore, this paper combines the above methods and realizes the preprocessing of foggy image through the combination of histogram equalization and guided filtering.
x represents the original image of the original diagram, and y denotes the average pixel gray level of the histogram of the square diagram. Normalize x and y so that [TeX:] $$0 \leq x, y \leq 1.$$ Normalize any foggy image and control its gray level between [TeX:] $$0 \leq x \leq 1.$$ T transform any value of x within the range of [0,1] as follows (1):
where, for [TeX:] $$0 \leq x \leq 1$$, there is [TeX:] $$0 \leq y \leq 1$$.
In the range of [TeX:] $$0 \leq x \leq 1$$, [TeX:] $$T(x)$$ is a monotonically increasing function. Inverse transformation to (2):
Wherein, [TeX:] $$0 \leq y \leq 1$$ satisfies the condition of formula (1) above.
The probability density of x is defined as [TeX:] $$P_x(x)$$; The probability density of y is obtained from the following formula (3):
Suppose the transformation function is (4)
where w represents the integral variable and [TeX:] $$\int_0^x P_x(w) d w$$ represents the cumulative distribution function of x. The derivative of x is showed as follow:
Bring back the results obtained from Eq. (5) to the above Eq. (3):
(6)
[TeX:] $$\left.\left.\left.P_y(x)=\left[P_x(x) \frac{d x}{d y}\right)\right] \mid x=T^{-1}(y)=\left[P_x(x) \frac{1}{d y / d x}\right)\right] \mid x=T^{-1}(y)=\left[P_x(x) \frac{1}{P_x(x)}\right)\right] \mid=1.$$From the above derivation process and the obtained results (6), it can be seen that with the transformation y distribution gradually uniform and smooth, corresponding to the image level, it is to expand the range of pixel values. From a mathematical point of view, histogram equalization is the transformation correction of cumulative distribution function.
3. Research on Image Enhancement Algorithm and its Application in Image Defogging
3.1 Image Enhancement
In foggy weather, small water droplets in the air combine with suspended particles, resulting in a large particle radius in the atmospheric composition and a strong influence on sunlight. The image taken under the influence of insufficient light is not clear enough and blurred, and the problem can be solved by image defogging technology.
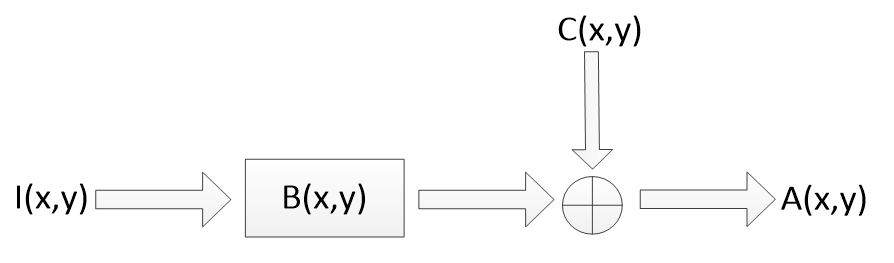
In most cases, the fog image attenuation model can be decomposed into degradation function term and additive white noise term. For foggy image [TeX:] $$I(x, y)$$, the essence of image restoration is to estimate the real image [TeX:] $$J(x, y)$$ of the real scene without fog according to the foggy image. For the degraded image [TeX:] $$A(x, y)$$ of the fog map, according to the degraded image [TeX:] $$A(x, y)$$, the degraded function term [TeX:] $$B(x, y)$$ and the additive white noise [TeX:] $$C(x, y)$$, the more data of A and B are obtained, and the obtained [TeX:] $$J(x, y)$$ is closer to the fog free map of the real scene. Fig. 1 shows a general model of image attenuation.
Assuming the image attenuation is linearly constant, the degraded image can be described by Eq. (7):
The form of convolution kernel in spatial domain. From the viewpoint of mathematics, image enhancement is the process of finding a transformation relationship or operation relationship D, transforming I into D and obtaining B, as shown in formula (8):
Then inverse transform the image to estimate the real image, as shown in Eq. (9):
Whether the image restoration can obtain the approximate estimation of the real scene image must consider the fit between the established mathematical model and the physical application. If this model is applied to fog image restoration step by step, there are still several problems:
Poor overall consideration.
The degenerate function cannot be evaluated.
Not targeted.
The above factors explain the reasons for the decay of demist images. Starting from the formation mechanism of fog image can establish the physical model of fog attenuation image to get better image defogging effect.
3.2 Enhance the Visual Effect of Defogging Image
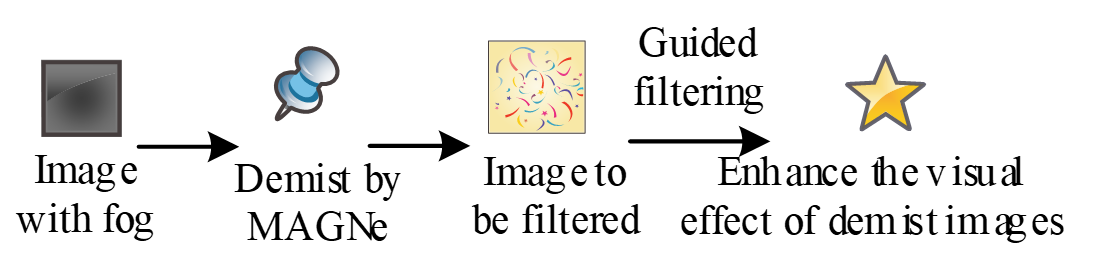
With wide application of depth neural network, the existing defogging methods can remove most of the fog in the real image, but the defogging image has the problems of loss of detail information and reduced visual effect. For this, it can be applied to guided filtering for image defogging, as shown in Fig. 2.
Fig. 2 applies MAGNe and guided filtering. Guided filtering can maintain the edge characteristics. Guided filtering describes the relationship between the guided image I and the output image q as a local linear model.
A complex function can be represented by many local linear functions. When calculating the value of a point on the function, it only needs to calculate the values of all linear functions containing the point and average them. Therefore, it can be assumed that the output and input of the function conform to a linear relationship in a two-dimensional window, as shown in (10):
In formula (10), q represents the value of the output pixel, I represents the value of the input image, i and k are the pixel indexes, and a and b represent the coefficients of the linear function when the window center is located at k.
The input image can be the image to be filtered itself and the guide image as well. Take the gradient on both sides of the above formula, and you can get the result as shown in formula (11):
When the input image I has a gradient, the output q also has a similar gradient, so the guided filtering has the characteristic of edge preservation. The image after fog removal by MAGNe is used as the image to be filtered p and the guide image I, and the visual effect of the fog removal image is enhanced by guide filtering. The definition of the method is shown in formula (12):
(12)
[TeX:] $$Q_k=\frac{1}{\left|\omega_k\right|^2} \sum_{(i, j) \in \omega_k} P_k\left(1+\frac{\left(I_i-\mu_k\right)\left(I_j-\mu_k\right)}{\sigma_k^2+\varepsilon}\right).$$In formula (12), [TeX:] $$\omega_k$$ is the window centered on pixel k in the guide image (hereinafter referred to as the window), [TeX:] $$\left|\omega_k\right|$$ represents the number of pixels, [TeX:] $$\mu_k$$ represents the average value of pixel values of each pixel in the window, [TeX:] $$I_i \text{ and } I_j$$ are the brightness values of two adjacent pixels of pixel k in the guide image, [TeX:] $$\sigma_k$$ is the variance of pixel values corresponding to pixel points in the window, and [TeX:] $$\varepsilon$$ is the adjustment coefficient. According to the method of formula (12), each pixel in the guide image and the image to be filtered is traversed, thus enhancing the visual effect of the defogging image.
4. Experiment
4.1 Experimental Design
PyTorch is a deep learning framework commonly used in Python. It is a tensor and dynamic neural network in Python language. It contains a mixture of high-level API and low-level API, and can also be accelerated by GPU. PyTorch is based on Torch. The design of PyTorch aims at least encapsulation and is characterized by flexibility, efficiency, and speed. It conforms to human thinking and is adopted by many institutions. The image defogging methods in this paper are based on the idea of image enhancement, and the PyTorch framework is used as the basic framework of this method. In [7] and [8], the authors are used as the comparison algorithm of the methods used in the article. The relevant information of these three methods is shown in Table 1.
Table 1.
| Project | He et al. [7] | Wang et al. [8] | Present study |
|---|---|---|---|
| Experimental platform | MATLAB R2016a | MATLAB R2016a | MATLAB R2016a |
| Usage method | Image defogging method based on MALLAT algorithm | Single image defogging algorithm based on neural network ooptimization | Physical model and guided filtering of fog attenuation image |
| Evaluating indicator | PSNR and SSIM | PSNR and SSIM | PSNR and SSIM |
| Fog image format | PNG | PNG | PNG |
| Image size with fog | 389×729 | 389×729 | 389×729 |
4.2 Experimental Index
To evaluate the defogging effect of the proposed method on synthetic images, two image quality evaluation indices: peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) were used as indicators.
4.2.1 PSNR
Among them, PSNR realizes the evaluation of the overall similarity of the image, which is mainly based on the calculation of the error between the corresponding pixels between the defog image and the non-fog image, which focuses on the evaluation of the color deviation of the defog image and the distortion of the defog image. The larger the value of PSNR, the smaller the distortion of the defog image and the closer to the fog free image. The calculation method of PSNR is shown in formula (13):
(13)
[TeX:] $$P S N R=10 \times \log _{10}\left(\frac{M A X_I^2}{M S E}\right)=20 \times \log _{10}\left(\frac{M A X_I}{\sqrt{M S E}}\right).$$In formula (13), MSE denotes the mean square error; [TeX:] $$M A X_I$$ denotes the maximum value in the image color value, which is usually 255.
4.2.2 Structural similarity
SSIM is an index reflecting the similarity between defog images and non-fog images. Three different standards of brightness, contrast and structure are used to evaluate the similarity of the two images. The larger the SSIM value, the more similar the defog image and non-fog image, and the better the defog effect. The calculation method of SSIM is shown in formula (14):
(14)
[TeX:] $$\operatorname{SSIM}(x, y)=\frac{\left(2 \mu_x \mu_y+C_1\right)\left(2 \sigma_{x y}+C_2\right)}{\left(\mu_x^2+\mu_y^2+C_1\right)\left(\sigma_x^2+\sigma_y^2+C_2\right)},$$here [TeX:] $$\mu_x \text { and } \mu_y$$ denote the mean values of x and y, respectively; [TeX:] $$\sigma_x^2, \sigma_y^2$$ denotes the variance of x and y, respectively; [TeX:] $$\sigma_{xy}$$ denotes the covariance of x and y; [TeX:] $$C_1 \text{ and } C_2$$ denote two constants, which exist to prevent the denominator from being zero, resulting in system errors.
In order to obtain a better experimental defogging effect, the batch size in the experiment is set to 24. For the network optimization algorithm, the Adam algorithm is used to optimize the proposed method network, and the learning rate is set to 0.001. At the same time, the total number of training iterations of the proposed method is set to 3,000. The test data set consists of 700 images of different scenes taken on foggy days. The ratio between the test and training sets is 6:1. Once the entire dataset is trained, it is considered as one epoch, with a total of 50 epochs.
4.3 Experimental Result
4.3.1 Image enhancement effect comparison
The image enhancement processing effects of the methods in references [7,8] and the method proposed in this study were comparatively analyzed.
The method in [7] has a significant enhancement effect on images with low illumination, which is not sufficient to restore the overall brightness. Local objects are too dark, but the enhanced image color is not natural enough. The method in [8] makes the color of the enhanced image white, which is not in accordance with the real visual effect; The enhancement effect of the proposed algorithm is natural in brightness recovery, and has a significant improvement in image detail texture recovery, which is in accordance with the normal visual effect. The contour and detail of the image retain more information (Fig. 3).
Fig. 3.

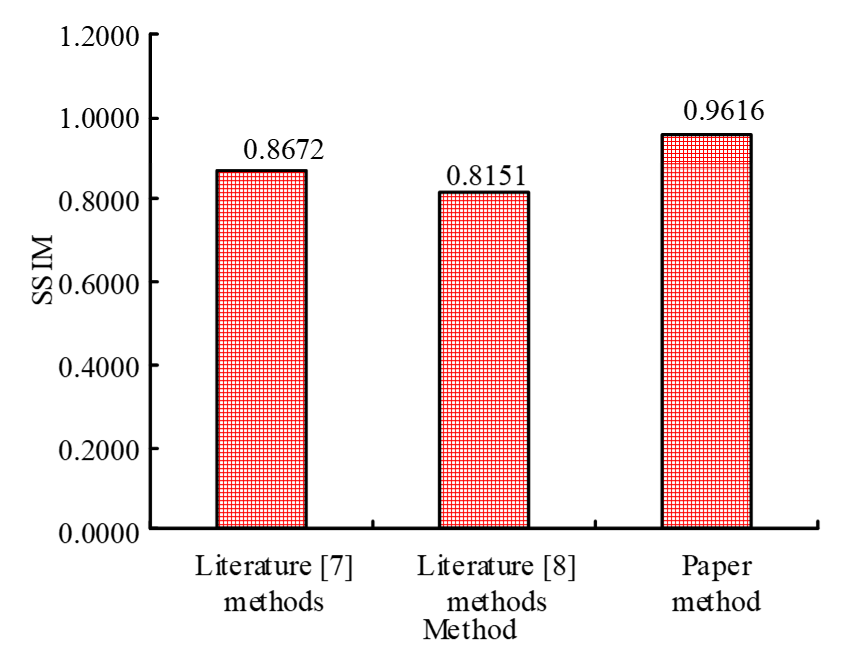
4.3.2 SSIM
To prove the image demisting effect of the proposed method in this study, three methods (He et al. [7], Wang et al. [8], and this study) are used to detect the SSIM value of the image after demisting.
It can be seen from Fig. 4 that the SSIM value of the method in this paper is the largest, with the SSIM value of 0.9616, which is 0.0944 higher than the SSIM value in [7], while the SSIM value in [8] is 0.8151. It can be seen that the image defogging effect of this method is better.
4.3.3 PSNR
To demonstrate the image defogging effect of the proposed method, three methods (He et al. [7], Wang et al. [8], and this study) are used to detect the image peak SNR after defogging.
According to the analysis of Table 2, when the number of training iterations is 500, the image PSNR of the method in [7] is 31.68 dB, the image PSNR of the method in [8] is 22.41 dB, and the image PSNR of the method in this paper is 32.63 dB. When the number of training iterations is 1,500, the image PSNR of the method in [7] is 15.74 dB, the image PSNR of the method in literature [8] is 12.76 dB, and the image PSNR of the proposed method is 16.68 dB. When the number of training iterations is 3000, the image PSNR of the method in [7] is 35.68 dB, the image PSNR of the method in [8] is 38.38 dB, and the image PSNR of the proposed method is 43.29 dB. The image PSNR of this method is much higher than that of other methods, which shows that the image defogging effect of this method is better.
5. Conclusion
This paper studies an image enhancement algorithm and image defogging method. The fog image is preprocessed by histogram equalization method; The physical model of atmospheric scattering is constructed, the image detail feature is enhanced by image enhancement method, and the visual effect of defogging image is enhanced by guided filtering method. The proposed method has a good defogging effect on the image.
When the number of training iterations is 3000, the image PSNR of this method is 43.29 dB. The image PSNR of the proposed method is much higher than that of other methods.
When the number of training iterations is 3,000, the similarity of image structure after defogging is 0.9616. After defogging, the image structure similarity of the proposed method is significantly higher than that of other methods, indicating better image-defogging effect.
Biography
Jun Cao
https://orcid.org/0000-0002-2256-5083She was born in Sichuan, China, in 1984. She received her bachelor’s degree in computer science and technology from Southwest University in 2006, and master’s degree in computer technology from Chongqing Normal University in 2017. Currently, she is a lecturer at Guang'an Vocational & Technical College. She has published a total of 6 papers. Her research interest covers image processing.
References
- 1 B. Zhao, "Plateau environment and urban planning based on image defogging algorithm," Arabian Journal of Geosciences, vol. 14, article no. 1472, 2021. https://doi.org/10.1007/s12517-021-07727-7doi:[[[10.1007/s12517-021-07727-7]]]
- 2 S. He, Z. Chen, F. Wang, and M. Wang, "Integrated image defogging network based on improved atmospheric scattering model and attention feature fusion," Earth Science Informatics, vol. 14, pp. 2037-2048, 2021. https://doi.org/10.1007/s12145-021-00672-9doi:[[[10.1007/s1-021-00672-9]]]
- 3 W. Liu, F. Zhou, T. Lu, J. Duan, and G. Qiu, "Image defogging quality assessment: real-world database and method," IEEE Transactions on Image Processing, vol. 30, pp. 176-190, 2020. https://doi.org/10.1109/TIP . 2020.3033402doi:[[[10.1109/TIP.2020.3033402]]]
- 4 S. Salazar-Colores, E. U. Moya-Sanchez, J. M. Ramos-Arreguin, E. Cabal-Yepez, G. Flores, and U. Cortes, "Fast single image defogging with robust sky detection," IEEE Access, vol. 8, pp. 149176-149189, 2020. https://doi.org/10.1109/ACCESS.2020.3015724doi:[[[10.1109/ACCESS.2020.3015724]]]
- 5 Z. Jiang, X. Sun, and X. Wang, "Image defogging algorithm based on sky region segmentation and dark channel prior," Journal of Systems Science and Information, vol. 8, no. 5, pp. 476-486, 2020. https://doi.org/ 10.21078/JSSI-2020-476-11doi:[[[10.21078/JSSI-2020-476-11]]]
- 6 J. You, P . Liu, and X. Rong, B. Li, and T. Xu, "Dehazing and enhancement research of polarized image based on dark channel priori principle," Laser & Infrared, vol. 50, no. 4, pp. 493-500, 2020.custom:[[[-]]]
- 7 H. He, A. Tuerhongjiang, and X. He, "An image defogging method based on MALLA T algorithm," Journal of Xinjiang Normal University (Natural Sciences Edition), vol. 39, no. 1, pp. 23-27, 2020.custom:[[[-]]]
- 8 X. Wang, D. Fang, H. He, and Q. Zou, "MSRCR image defog algorithm based on multi-scale detail optimization," Experimental Technology and Management, vol. 37, no. 9, pp. 92-97, 2020.custom:[[[-]]]
- 9 N. Hassan, S. Ullah, N. Bhatti, H. Mahmood, and M. Zia, "A cascaded approach for image defogging based on physical and enhancement models," Signal, Image and Video Processing, vol. 14, pp. 867-875, 2020. https://doi.org/10.1007/s11760-019-01618-xdoi:[[[10.1007/s11760-019-01618-x]]]
- 10 A. Sabir, K. Khurshid, and A. Salman, "Segmentation-based image defogging using modified dark channel prior," EURASIP Journal on Image and Video Processing, vol. 2020, article no. 6, 2020. https://doi.org/ 10.1186/ s13640-020-0493-9doi:[[[10.1186/s13640-020-0493-9]]]
- 11 Y . Yang, C. Zhang, P . Jiang, and H. Y ue, "Attention-based end-to-end image defogging network," Electronics Letters, vol. 56, no. 15, pp. 759-761, 2020. https://doi.org/10.1049/el.2020.1128doi:[[[10.1049/el.2020.1128]]]
- 12 D. Singh and V . Kumar, "Single image defogging by gain gradient image filter," Science China Information Sciences, vol. 62, article no. 79101, 2019. https://doi.org/10.1007/s11432-017-9433-4doi:[[[10.1007/s11432-017-9433-4]]]